We have not yet discussed how to integrate rational functions (recall that a rational
function is a function of the form f (x)/g(x), where f, g are polynomials). The
method that allows us to do so, in certain cases, is called partial fraction
decomposition.
Here we demonstrate this procedure in the case where the denominator g(x) is a product
of two distinct linear factors. This method can easily be generalized to the case where
g is a product of arbitrarily many distinct linear factors. The cases where g has
repeated linear factors or factors of degree 2 are slightly more complicated and will
not be considered.
The first step is to divide the polynomial f by the polynomial g to obtain
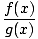 = h(x) + = h(x) + 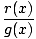 |
|
where h(x) and r(x) are polynomials, with the degree of r strictly less than the
degree of g. There is a result called the division algorithm that guarantees that we can do
this. Since we know how to integrate polynomials, we are left with figuring out how to
integrate r(x)/g(x). Multiplying the numerator and denominator by a constant, we may
assume that g(x) is of the form g(x) = (x - a)(x - b). Since the degree of r is less that
2, we may write it as r(x) = cx + d.
We want to write r(x)/g(x) in the form
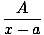 + + 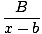 |
|
since we know how to integrate functions of this form (by change of variables, for
example). Multiplying the equation
by (x - a)(x - b) on each side and regrouping terms, we obtain
| cx + d | = | A(x - b) + B(x - a) |
|
| | = | (A + B)x + (- Ab - Ba) |
|
Setting the coefficients of the two polynomials equal to each other, we get a system of
two linear equations in the two variables A and B:
| A + B | = | c |
|
| (- b)A + (- a)B = d | | |
|
Since a≠b, this system has a solution. Now that we have done
all the hard work, we can easily calculate the integral:
 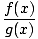 dx dx | = |  h(x)dx + h(x)dx +  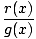 dx dx |
|
| | = |  h(x)dx + h(x)dx +  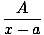 dx + dx +  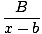 dx dx |
|