The following formulas relate the products of sines and cosines to sines and
cosines of multiple angles. These formulas are derived from the addition
formulas. They are useful
identities for simplification.
sin(α)sin(β) = - 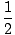 (cos(α + β) - cos(α - β)) (cos(α + β) - cos(α - β)) |
|
cos(α)cos(β) = 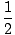 (cos(α + β) + cos(α - β)) (cos(α + β) + cos(α - β)) |
|
sin(α)cos(β) = 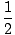 (sin(α + β) + sin(α - β)) (sin(α + β) + sin(α - β)) |
|
cos(α)sin(β) = 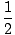 (sin(α + β) - sin(α - β)) (sin(α + β) - sin(α - β)) |
|