| Addition of Angles | sin(α + β) = sin(α)cos(β) + cos(α)sin(β);cos(α + β) = cos(α)cos(β) - sin(α)sin(β);tan(α + β) = 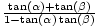 |
| Double Angle | sin(2x) = 2 sin(x)cos(x);cos(2x) = cos2(x) - sin2(x) = 1 - 2 sin2(x) = 2 cos2(x) - 1;tan(2x) = 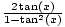 |
| Function Products | sin(α)sin(β) = - 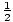 (cos(α + β) - cos(α - β));cos(α)cos(β) = (cos(α + β) - cos(α - β));cos(α)cos(β) = 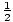 (cos(α + β) + cos(α - β));sin(α)cos(β) = (cos(α + β) + cos(α - β));sin(α)cos(β) = 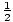 (sin(α + β) + sin(α - β));cos(α)sin(β) = (sin(α + β) + sin(α - β));cos(α)sin(β) = 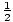 (sin(α + β) - sin(α - β)) (sin(α + β) - sin(α - β)) |
| Function Sums and Differences | sin(α) + sin(β) = 2 sin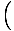 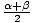 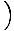 cos cos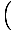 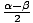 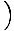 ;cos(α) + cos(β) = 2 cos ;cos(α) + cos(β) = 2 cos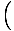 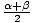 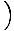 cos cos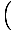 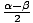 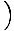 ;sin(α) - sin(β) = 2 cos ;sin(α) - sin(β) = 2 cos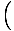 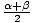 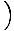 sin sin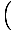 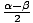 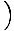 ;cos(α) - cos(β) = - 2 sin ;cos(α) - cos(β) = - 2 sin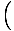 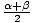 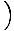 sin sin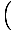 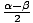 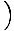 |
| Half Angle | sin(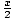 ) = ± ) = ±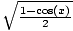 ;cos( ;cos(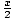 ) = ± ) = ±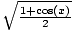 ;tan( ;tan(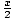 ) = ± ) = ±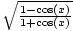 = = 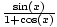 = = 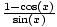 |
| Subtraction of Angles | sin(α - β) = sin(α)cos(β) - cos(α)sin(β);cos(α - β) = cos(α)cos(β) + sin(α)sin(β);tan(α - β) = 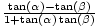 . .
|













