Previous Next

Equation 2: The Impulse-Momentum Theorem

The second equation we can generate from our definition of momentum comes from our equations for impulse. Recall that:

J = mvf - mvo

Substituting our expression for momentum, we find that:

J = pf - po = Δp    

This equation is known as the Impulse-Momentum Theorem. Stated verbally, an impulse given to a particle causes a change in momentum of that particle. Keeping this equation in mind, momentum is conceptually quite similar to kinetic energy. Both quantities are defined based on concepts dealing with force: kinetic energy is defined by work, and momentum is defined by impulse. Just as a net work causes a change in kinetic energy, a net impulse causes a change momentum. In addition, both are related to velocity in some way. In fact, combining the two equations K = mv2 and p = mv we can see that:

K =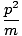    

This simple equation can be quite convenient for relating the two different concepts.

This section, dealing exclusively with the momentum of a single particle, might seem out of place after a section on systems of particles. However, when we combine the definition of momentum with our knowledge of systems of particles, we can generate a powerful conservation law: the conservation of momentum.

Previous page Impulse and Momentum page 1 Next section

Take a Study Break