Problem :
Calculate the center of mass of the following system: A mass of 5 kg lies at x = 1, a mass of 3 kg lies at x = 4 and a mass of 2 kg lies at x = 0.
We need only do a simple calculation:
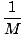 (m1x1 + m2x2 + m3x3) =
(m1x1 + m2x2 + m3x3) = 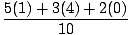 = 1.7
= 1.7
Problem :
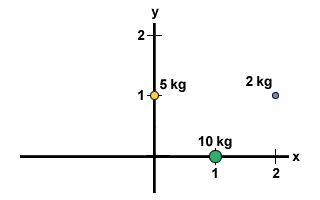
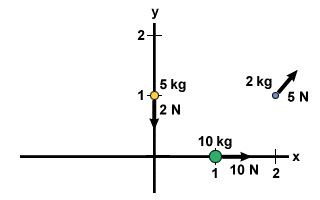
Calculate the center of mass of the following system: A mass of 10 kg lies at
the point (1,0), a mass of 2 kg lies at the point (2,1) and a mass of 5 kg lies
at the point (0,1), as shown in the figure below.
To find the center of mass in a two dimensional system, we must complete two steps. First we must find the center of mass in the x-direction, and then in the y-direction. We know that the total mass of the system is 17 kg. Thus:
| xcm | = | 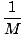 (m1x1 + m2x2 + m3x3) (m1x1 + m2x2 + m3x3) | |
| = | 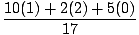 = = 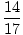 = .824 = .824 |
Also, then
| ycm | = |  (m1y1 + m2y2 + m3y3) (m1y1 + m2y2 + m3y3) | |
| = | 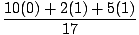 = =  = .412 = .412 |
Thus the center of mass of the system lies at the point (.824, .412).
Problem :
Consider the system from problem 2, but now with forces acting upon the system.
On the 10 kg mass, there is a force of 10 N in the positive x direction. On the
2 kg mass, there is a force of 5 N inclined 45o above horizontal.
Finally, on the 5 kg mass, there is a force of 2 N in the negative y direction.
Find the resultant acceleration of the system.
Since we already know the position of the center of mass and the total mass of
the system, we can use the equation  Fext = Macm to find the
acceleration of the system. To do so, we must find the net force by breaking
each force acting on the system into x and y components:
Fext = Macm to find the
acceleration of the system. To do so, we must find the net force by breaking
each force acting on the system into x and y components:
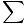 Fx = 10 + 5 cos 45 = 13.5 N Fx = 10 + 5 cos 45 = 13.5 N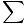 Fy = 5 sin 45 - 2 = 1.5 N Fy = 5 sin 45 - 2 = 1.5 N |
Thus the magnitude of the net force is given by:
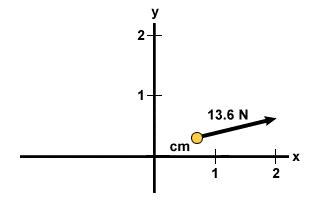
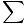 F =
F =  = 13.6 N
= 13.6 N
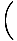
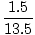
 = 6.3o
= 6.3o
Now that we have the resultant force on the system, we can find the acceleration of the system. To conceptualize this, we imagine that all the mass of the system is placed at the spot of the center of mass, and the net force acts on that spot. Thus:
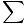 Fext = Macm
Fext = Macm
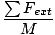 =
= 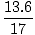 = .8 m/s2
= .8 m/s2
Problem :
Two masses, m1 and m2, m1 being larger, are connected by a spring. They are placed on a frictionless surface and separated so as to stretch the spring. They are then released from rest. In what direction does the system travel?
We can regard the two masses and the spring as an isolated system. The only force felt by the masses is the spring force, which lies inside the system. Thus no external force acts on the system, and the center of mass of the system is never accelerated. Thus, because the velocity of the center of mass is initially zero (as neither block is moving before they are released) this velocity must remain at zero. Though each block is accelerated by the spring in some way, the velocity of the center of mass of the system never changes, and the position of center of mass of the system never moves. The blocks will continue oscillating on the spring, but will not cause any translational motion of the system.
Problem :
A 50 kg man stands at the edge of a raft of mass 10 kg that is 10 meters long.
The edge of the raft is against the shore of the lake. The man walks toward the
shore, the entire length of the raft. How far from the shore does the raft move?

You may ask what this problem has to do with center of mass. Let's examine
closely exactly what is going on. Since we are talking about systems of
particles in this section, let's visualize this situation as a system. The man
and the raft are two separate objects, and mutually interact when the man walks
across the boat. Initially the boat is at rest, so the center of mass is a
stationary point. When the man walks across the boat, no external force acts on
the system, as the boat is allowed to glide across the water. Thus while the man
walks across the raft, the center of mass must stay in the same place. In
order to do so, the raft must move out from the shore a certain distance. We can
calculate this distance, which we shall denote by d, using center of mass
calcualtions.

We start be calculating the center of mass when the man is at point A. Remember that we can choose our origin, so we shall choose x = 0 to be at the shoreline. For this problem we can assume that the raft has a uniform density, and thus can be treated as if all its mass were at its midpoint, of x = 5. Thus the center of mass is:
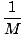 m1x1+m2x2 =
m1x1+m2x2 = 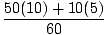 = 9.2 m
= 9.2 m
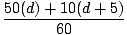 =
= 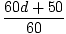
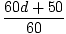 = 9.2 = 9.2 | |||
| 60d + 50 = 552 | |||
| d = 8.4 m |
Thus as the man moves from point A to point B, the raft gets displaced 8.4 meters from the shore.


 payment page
payment page



