Please wait while we process your payment
If you don't see it, please check your spam folder. Sometimes it can end up there.
If you don't see it, please check your spam folder. Sometimes it can end up there.
Please wait while we process your payment
Get instant, ad-free access to our grade-boosting study tools with a 7-day free trial!
Learn more



This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Create Account
Select Plan
Payment Info
Start 7-Day Free Trial!

Annual
2-49 accounts
$22.49/year + tax
50-99 accounts
$20.99/year + tax
Select Quantity
Price per seat
$29.99 $--.--
Subtotal
$-.--
Want 100 or more? Request a customized plan
You could save over 50%
by choosing an Annual Plan!

SAVE OVER 50%
compared to the monthly price!
| Focused-studying | ||
| PLUS Study Tools | ||
| AP® Test Prep PLUS | ||
| My PLUS Activity | ||
$22.49/month + tax
Save 25%
on 2-49 accounts
$20.99/month + tax
Save 30%
on 50-99 accounts
| Focused-studying | ||
| PLUS Study Tools | ||
| AP® Test Prep PLUS | ||
| My PLUS Activity | ||
No Fear provides access to Shakespeare for students who normally couldn’t (or wouldn’t) read his plays. It’s also a very useful tool when trying to explain Shakespeare’s wordplay!
Erika M.
I tutor high school students in a variety of subjects. Having access to the literature translations helps me to stay informed about the various assignments. Your summaries and translations are invaluable.
Kathy B.
Teaching Shakespeare to today's generation can be challenging. No Fear helps a ton with understanding the crux of the text.
Kay H.
No Fear provides access to Shakespeare for students who normally couldn’t (or wouldn’t) read his plays. It’s also a very useful tool when trying to explain Shakespeare’s wordplay!
Erika M.
I tutor high school students in a variety of subjects. Having access to the literature translations helps me to stay informed about the various assignments. Your summaries and translations are invaluable.
Kathy B.
Teaching Shakespeare to today's generation can be challenging. No Fear helps a ton with understanding the crux of the text.
Kay H.
Create Account
Select Plan
Payment Info
Start 7-Day Free Trial!
You will only be charged after the completion of the 7-day free trial.
If you cancel your account before the free trial is over, you will not be charged.
You will only be charged after the completion of the 7-day free trial. If you cancel your account before the free trial is over, you will not be charged.
Order Summary
Annual
7-day Free Trial
SparkNotes PLUS
$29.99 / year
Annual
Quantity
51
PLUS Group Discount
$29.99 $29.99 / seat
Tax
$0.00
SPARK25
-$1.25
25% Off
Total billed on Nov 7, 2024 after 7-day free trail
$29.99
Total billed
$0.00
Due Today
$0.00
Promo code
This is not a valid promo code
Card Details
By placing your order you agree to our terms of service and privacy policy.
By saving your payment information you allow SparkNotes to charge you for future payments in accordance with their terms.
Powered by stripe
Legal
Google pay.......



Please wait while we process your payment

Sorry, you must enter a valid email address
By entering an email, you agree to our privacy policy.
Please wait while we process your payment

Sorry, you must enter a valid email address
By entering an email, you agree to our privacy policy.
Please wait while we process your payment

Your PLUS subscription has expired
Please wait while we process your payment
Please wait while we process your payment

Definition of the Magnetic Field
With a brief history of electromagnetism, and a general understanding of what conditions give rise to a magnetic field, we may now precisely define the magnetic field.
When we defined the electric field, we first established the electric charge, and related the interaction of electric charges through Coulomb's Law. Unfortunately we cannot do the same for magnetic fields, because magnetic charges do not exist. Whereas electric fields originate from a single point charge, magnetic fields come from a wide variety of sources: currents in wires of varying shapes or forms, permanent magnets, etc. Instead of beginning with a description of the field created by each of these examples, we must define the magnetic field in terms of the force exerted by the field on a moving point charge.
Consider a point charge q moving with a velocity v that is perpendicular to the
direction of the magnetic field, as shown below.

In this very simple case, the force felt by the positive point charge has magnitude
F = 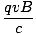 |
Take your right hand (it is important not to use the left one), and stick your thumb, your index finger and your middle finger in mutually perpendicular directions. Each one of these fingers represents a vector quantity: the thumb points in the direction of the velocity of the positively charged particle, the index finger points in the direction of the magnetic field, and the middle finger points in the direction of the force felt by the moving charge. Try it out on the above figure: point your thumb in the negative x direction and your index finger in the negative y direction. Hopefully you will find that your middle finger points in the positive z direction, which is exactly the direction of the force. This is known as the first right hand rule.
We disucussed the special case in which the moving charge moves perpendicular to the magnetic field. This perfectly perpendicular situation is uncommon. In more normal circumstances the magnetic force is proportional to the component of the velocity that acts in the perpendicular direction. If a charge moves with a velocity at an angle θ to the magnetic field, the force on that particle is defined as:
F = 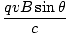 |
forceequation*
 = = 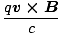 |
Please wait while we process your payment





