Problem : At what point during the oscillation of a spring is the force on the mass greatest?
Recall that F = - kx. Thus the force on the mass will be greatest when the displacement of the block is maximum, or when x = ±xm.Problem : What is the period of oscillation of a mass of 40 kg on a spring with constant k = 10 N/m?
We have derived that T = 2Π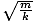 . To find the period of
oscillation we simply plug into this equation:
. To find the period of
oscillation we simply plug into this equation:
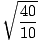 = 4Π seconds
= 4Π seconds
Problem :
A mass of 2 kg is attached to a spring with constant 18 N/m. It is then displaced to the point x = 2. How much time does it take for the block to travel to the point x = 1?
For this problem we use the sin and cosine equations we derived for simple
harmonic motion. Recall that x = xmcos(σt). We are given x and xm
in the question, and must calculate σ before we can find t. We know,
however, that no matter the initial displacement,
σ = 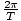 =
= 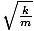 =
= 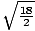 = 3. Thus we can
plug in our values:
= 3. Thus we can
plug in our values:
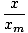 | = | cosσt | |
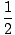 | = | cos3t | |
| 3t | = | cos-1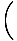 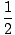 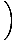 | |
| t | = | 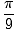 = .35 seconds = .35 seconds |
This problem was a simple example of how to use our equations for simple harmonic motion.
Problem :
A 4 kg mass attached to a spring is observed to oscillate with a period of 2 seconds. What is the period of oscillation if a 6 kg mass is attached to the spring?
To find the period of oscillation we need only know m and k. We are given m and must find k for the spring. If a 4 kg mass oscillates with a period of 2 seconds, we can calculate k from the following equation:
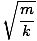
Implying that
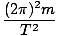 =
= 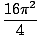 = 4Π2
= 4Π2
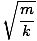 = 2Π
= 2Π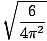 =
= 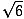 = 2.45
seconds
= 2.45
seconds
Problem :
A mass of 2 kg oscillating on a spring with constant 4 N/m passes through its equilibrium point with a velocity of 8 m/s. What is the energy of the system at this point? From your answer derive the maximum displacement, xm of the mass.
When the mass is at its equilibrium point, no potential energy is stored in the spring. Thus all of the energy of the system is kinetic, and can be calculated easily:
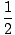 mv2 =
mv2 = 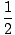 (2)(8)2 = 64 Joules
(2)(8)2 = 64 Joules
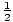 kxm2. Since energy is
conserved in the system, we can relate the answer we got for the energy at one
position with the energy at another:
kxm2. Since energy is
conserved in the system, we can relate the answer we got for the energy at one
position with the energy at another:
| Ef | = | Eo | |
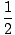 kxm2 kxm2 | = | 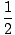 mv2 = 64 mv2 = 64 | |
| xm | = | 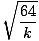 = =  = 4 meters = 4 meters |
We used energy considerations in this problem in much the same way we did when we first encountered conservation of energy- whether the motion is linear, circular or oscillatory, our conservation laws remain powerful tools.


 payment page
payment page



