Problem :
Most planets orbit the sun in elliptical orbits. Do these planets exhibit
rotational motion?
Rotational motion has two requirements: all particles must move about a fixed
axis, and move in a circular path. Since the path of most planets is not
circular, they do not exhibit rotational motion.
Problem :
A frisbee completes 100 revolutions every 5 seconds. What is the angular
velocity of the frisbee?
Recall that 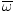 =
= 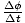 . We can assume
that the angular velocity is constant, so we can use this equation to solve our
problem. Each revolution corresponds to an angular displacement of 2Π
radians. Thus 100 revolutions corresponds to 200Π radians. Thus:
. We can assume
that the angular velocity is constant, so we can use this equation to solve our
problem. Each revolution corresponds to an angular displacement of 2Π
radians. Thus 100 revolutions corresponds to 200Π radians. Thus:
σ =
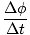
=
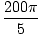
= 40
Π rad/s = 125.7 rad/s
Problem :
A car, starting from rest, accelerates for 5 seconds until its wheels are moving
with an angular velocity of 1000 rad/s. What is the angular acceleration of the
wheels?
Again, we can assume that the acceleration is constant, and use the following
equation:
α =
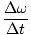
=
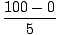
= 20 rad/s
2
Problem :
A merry-go-round is accelerated uniformly from rest to an angular velocity of 5
rad/s in a period of 10 seconds. How many times does the merry-go-round make a
complete revolution in this time?
We know that 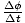 =
= 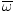 . Since we want to
solve for the total angular displacement, or φ, we rearrange this equation:
. Since we want to
solve for the total angular displacement, or φ, we rearrange this equation:
| Δφ | = | 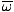 Δt Δt |
|
| | = | 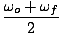 Δt Δt |
|
| | = | 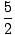 (10) (10) |
|
| | = | 25 rad/s |
|
However, we are asked for the number of revolutions, not the number of radians.
Since there are
2Π radians in every revolution, we divide our number by
2Π:
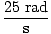
×
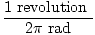
= 3.98 revolutions
Thus the merry-go-round revolves about 4 times in that period.