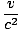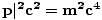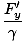Ad-free experience
Study Guides for 1,000+ titles
Full Text content for 250+ titles
No Fear Translations of Shakespeare’s plays (along with audio!) and other classic works
Flashcards
Mastery Quizzes
Infographics
Graphic Novels
AP® Practice & Lessons
Note-taking
Bookmarking
Dashboard
-
Relativistic energy
In Special Relativity the concept of total energy in the absence of a potential E = 1/2mv2 is replaced with another conserved quantity E = γmc2, where m is the mass or rest mass of the object. This quantity is conserved in all collisions and decays. Where there is a potential involved it is the total energy γmc2 + V which is conserved. Notice that an object at rest still has an amount of energy proportional to its mass Ev=0 = mc2.
-
Relativistic momentum
The quantity that is conserved in all collisions in relativity is not p = mv but p = γmv. This is called the relativistic momentum. When v < < c then γ
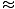1 and pmv.
-
4-vector
A vector with four components that, under a Lorentz transformation, transforms as (cdt, dx, dy, dz) does. That is, for A = (A0, A1, A2, A3) the 4-vector in another frame must be:
A0 = γ(A0' + (v/c)A1') A1 = γ(A1' + (v/c)A0') A2 = A2' A3 = A3'
Only those vectors for which the result of the above transformation is equal to the transformation of the individual coordinates under the Lorentz transformations are 4-vectors. The velocity 4-vector (γv, γbfv) and the energy-momentum 4-vector (E/c,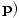
are the most common.
-
Proper time
The proper time interval between any two events is defined as:
Δτ =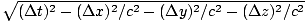 
This is a particularly useful quantity because it is in independent of the frame in which it is measured. -
Inner product invariance
The inner product of two 4-vectors is defined as:
AƒB = A0B0 - A1B1 - A2B2 - A3B3
Note that the minus signs make this inner product different from the usual dot product in 3-space. When defined in this way, the inner product of any two 4-vectors is a constant, independent of frame (that is, it is independent of the frame in which the vectors are written). -
Relativistic units
Are units in which c, the speed of light is given the value 1. This can be done in any number of ways; setting the unit of distance equal to 3×108 meters is one way. Setting the unit of distance as approximately 1 foot and the unit of time to 1 nanosecond also does the trick since the speed of light is approximately 1 foot/nanosecond. This simplifies calculations immensely. If you need to find an exact answer it is always possible to put the right number of factors of c back in at the end of a calculation by looking at the units and working out where factors of m/s are missing.
Terms
Formulae
| Lorentz Transformations for Energy and Momentum |
|
| Formula for Velocity in terms of Energy and Momentum |
|
= 
| Relativistic relationship between mass, energy, and momentum. (Specifically, this equation states that the square of the energy-momentum 4-vector is equal to m2c4.) The formula reduces to the familiar E = mc2 when the momentum p is zero. |
|
| Lorentz transformations for force undergoing a boost in the y-direction. |
|
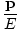