Thermodynamics: Heat: Heat Engines

Thermodynamics: Heat Heat Engines

Save

In fact, heat cannot be completely converted into work. Some heat must also be outputted as heat, to carry the entropy back out of the system. We can rewrite part of the thermodynamic identity as: σ_in = Q_in/τ_in. We want some of the input heat Q_in to be converted into work, so we know that Q_out will be less than Q_in.

We want all of the entropy to be extracted, however, and so we want σ_in = σ_out. The only way to accomplish such a feat is to have τ_in > τ_out. For this reason, we replace all of the "in" subscripts by "h", standing for "high temperature", and the "out" subscripts by "l", to indicate "low temperature".

Carnot Efficiency

The work that we actually get out in a heat engine is the difference between the input and output heat W = Q_h - Q_l = Q_h. Ideally, we would want W = Q_h, for in that case the system would be completely efficient.

For that reason, we define the Carnot efficiency, η_C, to be the ratio of the work to the input heat:

η_CâÉá

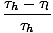
Carnot Inequality

Some processes occur within an engine that create entropy irreversibly. Friction is a good example of such an unwanted source of entropy. We therefore can say that the actual efficiency of an engine is only as good or worse than the Carnot efficiency: η≤η_C. This relation is known as the Carnot Inequality.

Therefore a heat engine is a device that takes an input of heat at a high temperature, converts the heat partially to work, and expels heat at a lower temperature to maintain constant entropy inside the device. The lower temperature cannot practically be lower than that of the environment because the heat must eventually be dumped somewhere. Therefore the higher temperature is typically quite hot, usually many hundreds of Kelvin.