The Quadratic Formula
Trinomials are not always easy to factor. In fact, some trinomials cannot be factored. Thus, we need a different way to solve quadratic equations. Herein lies the importance of the quadratic formula:
Given a quadratic equation ax2 + bx + c = 0, the solutions are given by the equation
x = 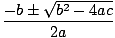 |
|
Example 1: Solve for x: x2 + 8x + 15.75 = 0
a = 1, b = 8, and c = 15.75.
x = 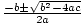
= 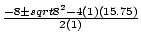
= 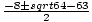
= 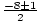
= 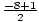 or
or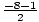
= - 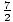 or-
or- 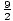
Thus,
x = - 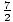
or
x = - 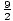
.
Example 2: Solve for x: 3x2 - 10x - 25 = 0.
a = 3, b = - 10, and c = - 25.
x = 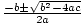
= 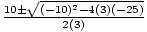
= 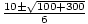
= 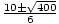
= 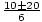
= 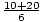 or
or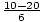
= 5 or- 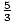
Thus,
x = 5 or
x = - 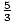
.
Example 3: Solve for x: -3x2 - 24x - 48 = 0.
a = - 3, b = - 24, and c = - 48.
x = 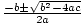
= 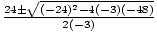
= 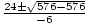
= 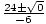
= 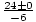
= 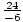 = - 4
= - 4
Thus,
x = - 4.
Example 4: Solve for x: 2x2 - 4x + 7.
a = 2, b = - 4, and c = 7.
x = 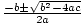
= 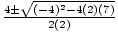
= 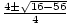
= 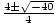
Since we cannot take the square root of a negative number, there are no solutions. (The graph of this quadratic polynomial will therefore be a parabola that never touches the
x-axis.)
The Discriminant
As we have seen, there can be 0, 1, or 2 solutions to a quadratic equation, depending on whether the expression inside the square root sign, (b2 - 4ac), is positive, negative, or zero. This expression has a special name: the discriminant.