-
Axis of Symmetry
The line which divides the parabola into two symmetrical halves. In the equation for the parabola y = a(x - h) + k, the axis of symmetry is x = h.
-
Completing the Square
A process by which we add and subtract a constant to create a perfect square trinomial within an equation and transform the equation of the form y = ax2 + bx + c into an equation of the form y = a(x - h)2 + k.
-
Discriminant
In the quadratic equation, the expression b2 - 4ac. The discriminant determines the number of solutions to a quadratic equation, or the number of x-intercepts of a quadratic function.
-
Parabola
The shape of the graph of y = a(x - h)2 + k.
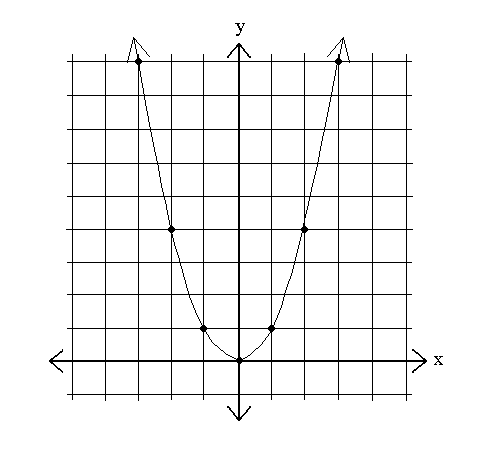
Graph of y = x2 -
Quadratic Equation
An equation of the form ax2 + bx + c = 0, where a≠ 0, and a, b, and c are real numbers.
-
Quadratic Formula
Given a quadratic equation ax2 + bx + c = 0, the solutions are given by the equation
x =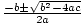
. -
Quadratic Function
A function of the form y = ax2 + bx + c, where a≠ 0, and a, b, and c are real numbers.
-
Vertex
In the equation y = a(x - h)2 + k, the point (h, k) -- the minimum point in a parabola that opens upward, or the maximum point in a parabola that opens downward.
