Previous Next

Here are the steps to completing the square, given an equation ax2 + bx + c:

  1. Compute d = .
  2. Add and subtract ad2 to the equation. This produces an equation of the form y = ax2 +2adx + ad2 - ad2 + c.
  3. Factor ax2 +2adx + ad2 into a(x + d )2. This produces and equation of the form y = a(x + d )2 - ad2 + c.
  4. Simplify ad2 + c. This produces an equation of the form y = (x - h)2 + k.
  5. Check by plugging the point (h, k) into the original equation. It should satisfy the equation.

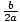Example 1: Complete the square: y = x2 + 6x - 12

a = 1, b = 6, c = - 12

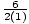  1. d = = 3
  2. ad2 = 9. y = (x2 + 6x + 9) - 9 - 12
  3. y = (x + 3)2 - 9 - 12
  4. y = (x + 3)2 - 21
  5. Check: -21 = (- 3)2 + 6(- 3) - 12

Example 2: Complete the square: y = 4x2 + 16x

a = 4, b = 16, c = 0

  1. d = = 2
  2. ad2 = 16. y = (4x2 + 16x + 16) - 16
  3. y = 4(x + 2)2 - 16
  4. y = 4(x + 2)2 - 16
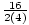  5. Check: -16 = 4(- 2)2 + 16(- 2)

Example 3: Complete the square: y = 2x - 28x + 100

a = 2, b = - 14, c = 100

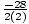  1. d = = - 7
  2. ad2 = 98. y = (2x - 28x + 98) - 98 + 100
  3. y = 2(x - 7)2 - 98 + 100
  4. y = 2(x - 7)2 + 2
  5. Check: 2 = 2(7)2 - 28(7) + 100

Example 4: Complete the square: y = - x2 + 10x - 1

a = - 1, b = 10, c = - 1

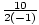  1. d = = - 5
  2. ad2 = - 25. y = (- x2 + 10x - 25) + 25 - 1
  3. y = - (x - 5)2 + 25 - 1
  4. y = - (x - 5)2 + 24
  5. Check: 24 = - 52 + 10(5) - 1

After we complete the square, we can graph the quadratic equation using the vertex.

Previous page Graphing Quadratic Functions page 1 Next section

Take a Study Break