Problem :
Sketch the graph of f (x) = 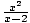 .
.
| f'(x) | = 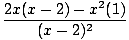 | ||
=  | |||
= 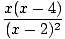 |
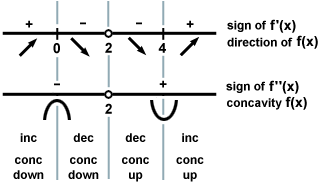
This equals zero when x = 0 or x = 4. The direction of f (x) based on the sign of the derivative is depicted below:

| f''(x) | =  | ||
= 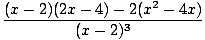 | |||
= 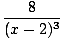 |
This never equals zero. The concavity of the graph is depicted below:

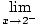 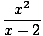 = - ∞ = - ∞ | |||
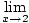 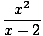 = ∞ = ∞ |
So, x = 2 is a vertical asymptote of the graph To find the horizontal asymptotes, take limits at infinity:
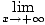 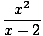 = + ∞ = + ∞ | |||
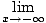 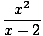 = - ∞ = - ∞ |
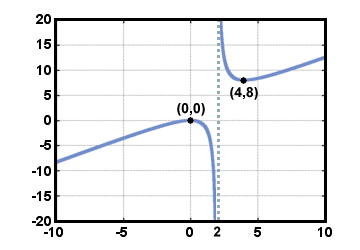
Thus, f grows without bound, and there are no horizontal asymptotes Now, find the exact coordinates of the intercepts and critical points: y-intercept: (0, 0)x-intercept: (0, 0) Critical Point: (0, 0) and (4, 8) Combining the information from the first derivative work and the second derivative work generates this single chart:
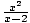
Problem :
Give a possible equation of the function graphed below:
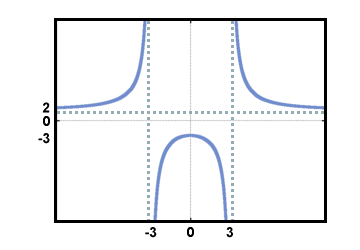
f (x) = 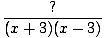 | |||
| This is the same as | |||
f (x) = 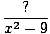 |
f has a horizontal asymptote at y = 2, which means that as x approaches infinity (or negative infinity), the function approaches 2. Thus, the function must look something like:
f (x) = 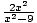
f (x) = 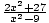
Problem :
Give a possible equation of the function graphed below:

f (x) = 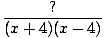 | |||
f (x) = 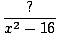 |
Because of the horizontal asymptotes,
f (x) = 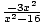
Problem :
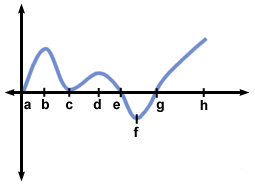
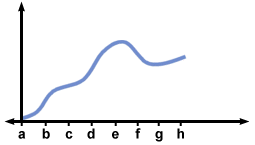
Below is a sketch of the graph of f'(x). Use this to sketch a possible graph of f (x).
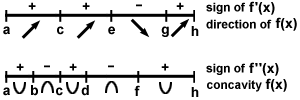
Did you know you can highlight text to take a note?
x


 payment page
payment page



