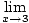  x3+4x x3+4x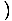 = 33 + 4(3) = 39 = 33 + 4(3) = 39 |
Rule 2:
 k = k wherek is a constant k = k wherek is a constant |
The limit of a constant function is the constant.
Rule 3:
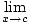  f (x)±g(x) f (x)±g(x) = =  f (x)± f (x)± g(x) g(x) |
The limit of a sum or difference of functions is equal to the sum or difference of the
individual limits.
Rule 4:
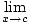  f (x)×g(x) f (x)×g(x) = = 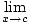 f (x)× f (x)×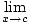 g(x) g(x) |
The limit of a product is equal to the product of the individual limits.
Rule 5:
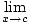 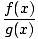 = = 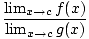 as long as as long as 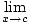 g(x)≠ 0 g(x)≠ 0 |
The limit of a quotient is equal to the quotient of the individual limits, as long as you don't end up dividing by zero.
Rule 6:
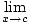   f (x) f (x)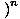 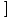 = = 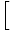 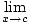 f (x) f (x) |
To find the limit of a function that has been raised to a power, we can first find the limit of the function, and then raise the limit to the power.
Using these limit rules in combination, you should be able to find the limits of many complex functions. For example, find
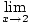      |
Solution:
The strategy here is to break the limit into simpler and simpler limits until we get to
limits that we can evaluate directly. By Limit Rule 6, we can evaluate the limit of the function
first and then raise the limit to the power later:
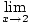      = =  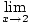    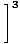 |
By Limit Rule 5, we can break up the limit of the rational function into the limit of the numerator divided by the limit of the denominator:
 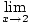   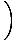 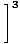 = =  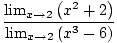  |
Finally, we are left with the limit of polynomial functions, which we can evaluate directly by Limit Rule 1:
 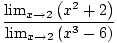  = =  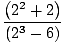  = =  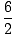  = 33 = 27 = 33 = 27 |
Two Additional Limit Techniques
In the example above, we used Limit Rule 5 for rational functions. But, as you'll recall,
this rules does not apply when the limit of the denominator equals zero. So what do we
do in this case? The following two techniques can help us when the limit of the
denominator goes to zero:
Technique 1: Factor and Reduce
Find
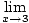 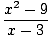 |
We can't use Limit Rule 5 here because the limit of the denominator as x approaches 3 is zero. However, we can factor the numerator and then reduce the fraction to get a limit we can evaluate:
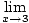 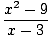 = =  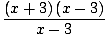 = =   x+3 x+3 = 6 = 6 |
Technique 2: Multiply by the Conjugate and Reduce
Find
  |
Again, the limit of the denominator goes to zero. Factoring also doesn't seem to work so well here, but we can multiply the numerator and denominator by the conjugate of the numerator and reduce the fraction into a limit we can evaluate:
  | =  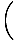  × ×  | ||
=  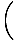   | |||
=  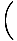 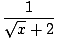 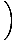 |
In the reduced fraction above, the limit of the denominator is no longer zero, so we can use Limit Rule 5 to solve for the limit:
 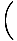 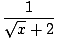  = = 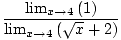 = = 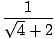 = =  |
The Squeeze Rule: Another Tool for Finding Limits
The squeeze rule can be a useful trick for evaluating limits when other methods just don't seem to work. It requires us to find one function that is always less than or equal to the function whose limit we're trying to evaluate, and another function that is always greater than or equal to our function.
Let's say we want to find the limit of a function h(x) as x approaches a certain value
c. Let f (x) be the function that we know to be less than or equal to h(x) for all x on
an open interval containing c, except possibly at x = c. Let g(x) be the function that we know to be greater than or
equal to h(x) for all x on an open interval containing c, except possibly at x = c.
What we have, then, is a situation where h(x) is "squeezed" between two functions
f (x) and g(x), i.e.
f (x)≤h(x)≤g(x).
The squeeze rule tells us that if f (x) and g(x) have the same limit as x approaches
c, then f (x), g(x), and h(x) must all be converging on the same point, so they
must therefore all have the same limit.
Example.
Find
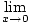 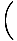 x4cos x4cos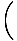 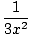   |
Note that we cannot use the product rule for limits here to evaluate this limit directly, since
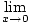 cos cos 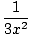  |
does not exist. This function will be an interesting example of a product of two functions where the limit of one of the functions doesn't exist, but the limit of the product does. To use the squeeze rule, we need to first find a function that is always less than or equal to
h(x) = x4cos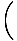 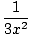  |
and a function that is always greater than or equal to it. One way to do this is to notice that this function is the product of x4 and
cos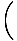 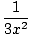  |
Although
cos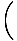 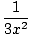  |
may look complicated and intimidating, it is still just a cosine function, and we know that cosine always falls between -1 and 1. Since the minimum value of
cos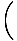 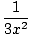  |
is -1, the function
h(x) = x4cos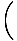 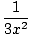  |
is always at least - x4. Similarly, the maximum value of
cos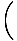 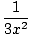  |
is 1, so the function
h(x) = x4cos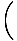 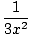  |
is always at most x4. We have established that
- x4≤x4cos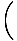 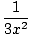  ≤x4, ≤x4, |
for all x, except possibly at x = 0. We are now ready to apply the squeeze rule:
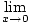  -x4 -x4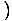 = 0 and = 0 and  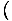 x4 x4 = 0 = 0 |
Therefore
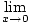 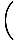 x4cos x4cos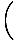 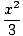   = 0 = 0 |
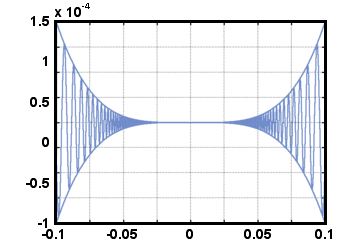
A picture of these three functions may help you understand what the squeeze rule is doing graphically:


 payment page
payment page



