payment page
-
Antiderivative
An antiderivative of a function f is any function F such that F' = f.
-
constant of integration
The constant term "+c" added to an antiderivative to indicate that there is not just one possible antiderivative, but an entire family of possible antiderivatives that differ by only a constant.
-
definite integral
Written as
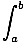f (x)dx
which is equal to the signed area under the curve of f on the interval [a, b]. These can be evaluated by the fundamental theorem of calculus. -
fundamental theorem of calculus
A theorem that provides a simple way to calculate definite integrals. It states: If F is an antiderivative of f, then
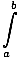f (x)dx=F(b) - F(a)
-
indefinite integral
Written as
f (x)dx
this represents the family of antiderivatives of the function f -
left-hand approximation
A type of Riemann sum in which the thin rectangles are of equal width, and in which the value of the function at the left endpoint of each subdivision is used as the height of the corresponding rectangle.
-
midpoint approximation
A type of Riemann sum in which the thin rectangles are of equal width, and in which the value of the function at the midpoint of each subdivision is used as the height of the corresponding rectangle.
-
Riemann sums
A method of approximating the area under the curve by dividing the region of interest into thin rectangles whose individual areas are calculated and summed to approximate the whole.
-
right-hand approximation
A type of Riemann sum in which the thin rectangles are of equal width, and in which the value of the function at the right endpoint of each subdivision is used as the height of the corresponding rectangle.
-
signed area
This is the area between the curve of f and the x-axis. It is called "signed" area because the area above the x-axis counts as positive, and the area below the x-axis counts as negative.
-
trapezoid rule
This is another method of calculating areas under curves by making subdivisions. Instead of using rectangles, the trapezoid rule uses thin trapezoids to generate an algorithm for approximating the area.
