Problem : Suppose there is a 10 foot ladder leaning against a wall, the base of which is being pulled away from the wall, along the ground, at a constant rate of 1 foot per second. The top of the ladder remains in contact with the wall as the base moves. How quickly is the top of the ladder sliding down the wall when it is 5 feet from the ground?
Let B(t) be the distance of the base of the ladder from the wall and let T(t) be the distance of the top of the ladder from the ground. These functions satisfy the relationg(t) = 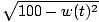 . . |
Differentiating each side with respect to t, we have
g'(t) = 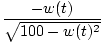 w'(t) w'(t) |
We are given that g'(t) = 1 and are interested in the situation when w(t) = 5. Solving for w'(t) above and plugging in these values, we find that the top of the ladder has velocity
| w'(t) | = | 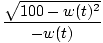 g'(t) g'(t) | |
| = | 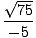 (1) (1) | ||
| = | - 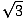 |
or approximately 1.73 feet per second downward. It is intriguing to note that as the top of the ladder approaches the ground, its speed approaches infinity, even though the bottom of the ladder continues to move away at a constant rate! (Realistically, at some point the bottom of the ladder will slip, the top crashing to the ground quite suddenly.)
Problem : Suppose you are given a magic rectangle, which can be stretched vertically or horizontally to change the lengths of its sides, but such that the area remains constant. You are given the rectangle in the form of a square, with each side have length 1 foot. To make sure the rectangle really is magic, you pull on it in one direction so that two opposite sides increase in length at a rate of 3 inches per second. Sure enough, the other two sides of the rectangle shrink to maintain the area of 1 square foot. How quickly are they shrinking when they are half their original length?
We choose to work in inches. Let a(t) be the length of the sides that are expanding at time t and b(t) the length of the sides that are shrinking. Then a(t)b(t) = 144. Solving for a(t) and differentiating each side with respect to t givesa'(t) = 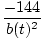 b'(t) b'(t) |
We are given that a'(t) = 3 and are interested in the moment when b(t) = 6. Solving for b'(t) and plugging in these values, we obtain
| b'(t) | = | 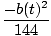 a'(t) a'(t) | |
| = | 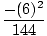 (3) (3) | ||
| = | 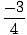 |
Thus the sides are shrinking at 3/4 inches per second when they are at half their original length.
Problem : Suppose a point is moving along the curve y = 3x2 - 2x from left to right at a horizontal speed of 2 units per second. How quickly is the y-coordinate of the point changing when the x-coordinate is at -1?
We differentiate each side of y = 3x2 - 2x with respect to t:| y'(t) = (6x(t) - 2)x'(t) |
Substituting x'(t) = 2 and x(t) = - 1, we obtain y'(t) = - 16.


 payment page
payment page



