Calculus BC: Applications of the Derivative: Analysis of Graphs

Figure %: Plot of f (x) = x³ and f'(x) = 3x²

The Second Derivative Test

Once we have found the critical points, one way to determine if they are local minima or maxima is to apply the first derivative test. Another way uses the second derivative of f. Suppose x₀ is a critical point of the function f (x), that is, f'(x₀) = 0. We have the following three cases:

f''(x₀) > 0 implies x₀ is a local minimum
f''(x₀) < 0 implies x₀ is a local maximum
f''(x₀) = 0 is inconclusive

The first two of these options derive from the observation that f''(x₀) is the rate of change of f'(x) at x₀, which will be positive if the derivative crosses zero from negative to positive, and negative is the derivative crosses zero from positive to negative. This is called the second derivative test for maxima and minima. The third, inconclusive case is considered below.

The first and second derivative tests employ essentially the same logic, examining what happens to the derivative f'(x) near a critical point x₀. The first derivative test says that maxima and minima correspond to f' crossing zero from one direction or the other, which is indicated by the sign of f' near x₀. The second derivative test is just the observation that the same information is encoded in the slope of the tangent line to f'(x) at x₀.

Concavity and Inflection Points

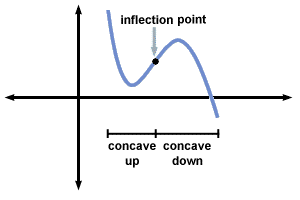
A function f (x) is called concave up at x₀ if f''(x₀) > 0, and concave down if f''(x₀) < 0. Graphically, this represents which way the graph of f is "turning" near x₀. A function that is concave up at x₀ lies above its tangent line in a small interval around x₀ (touching but not crossing at x₀). Similarly, a function that is concave down at x₀ lies below its tangent line near x₀.

The remaining case is a point x₀ where f''(x₀) = 0, which is called an inflection point. At such a point the function f holds closer to its tangent line than elsewhere, since the second derivative represents the rate at which the function turns away from the tangent line. Put another way, a function usually has the same value and derivative as its tangent line at the point of tangency; at an inflection point, the second derivatives of the function and its tangent line also agree. Of course, the second derivative of the tangent line function is always zero, so this statement is just that f''(x₀) = 0.

Inflection points are the critical points of the first derivative f'(x). At an inflection point, a function may change from being concave up to concave down (or the other way around), or momentarily "straighten out" while having the same concavity to either side. These three cases correspond, respectively, to the inflection point x₀ being a local maximum or local minimum of f'(x), or neither.