Please wait while we process your payment
If you don't see it, please check your spam folder. Sometimes it can end up there.
If you don't see it, please check your spam folder. Sometimes it can end up there.
Please wait while we process your payment
Get instant, ad-free access to our grade-boosting study tools with a 7-day free trial!
Learn more



This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Create Account
Select Plan
Payment Info
Start 7-Day Free Trial!

Annual
2-49 accounts
$22.49/year + tax
50-99 accounts
$20.99/year + tax
Select Quantity
Price per seat
$29.99 $--.--
Subtotal
$-.--
Want 100 or more? Request a customized plan
You could save over 50%
by choosing an Annual Plan!

SAVE OVER 50%
compared to the monthly price!
| Focused-studying | ||
| PLUS Study Tools | ||
| AP® Test Prep PLUS | ||
| My PLUS Activity | ||
$22.49/month + tax
Save 25%
on 2-49 accounts
$20.99/month + tax
Save 30%
on 50-99 accounts
| Focused-studying | ||
| PLUS Study Tools | ||
| AP® Test Prep PLUS | ||
| My PLUS Activity | ||
No Fear provides access to Shakespeare for students who normally couldn’t (or wouldn’t) read his plays. It’s also a very useful tool when trying to explain Shakespeare’s wordplay!
Erika M.
I tutor high school students in a variety of subjects. Having access to the literature translations helps me to stay informed about the various assignments. Your summaries and translations are invaluable.
Kathy B.
Teaching Shakespeare to today's generation can be challenging. No Fear helps a ton with understanding the crux of the text.
Kay H.
No Fear provides access to Shakespeare for students who normally couldn’t (or wouldn’t) read his plays. It’s also a very useful tool when trying to explain Shakespeare’s wordplay!
Erika M.
I tutor high school students in a variety of subjects. Having access to the literature translations helps me to stay informed about the various assignments. Your summaries and translations are invaluable.
Kathy B.
Teaching Shakespeare to today's generation can be challenging. No Fear helps a ton with understanding the crux of the text.
Kay H.
Create Account
Select Plan
Payment Info
Start 7-Day Free Trial!
You will only be charged after the completion of the 7-day free trial.
If you cancel your account before the free trial is over, you will not be charged.
You will only be charged after the completion of the 7-day free trial. If you cancel your account before the free trial is over, you will not be charged.
Order Summary
Annual
7-day Free Trial
SparkNotes PLUS
$29.99 / year
Annual
Quantity
51
PLUS Group Discount
$29.99 $29.99 / seat
Tax
$0.00
SPARK25
-$1.25
25% Off
Total billed on Nov 7, 2024 after 7-day free trail
$29.99
Total billed
$0.00
Due Today
$0.00
Promo code
This is not a valid promo code
Card Details
By placing your order you agree to our terms of service and privacy policy.
By saving your payment information you allow SparkNotes to charge you for future payments in accordance with their terms.
Powered by stripe
Legal
Google pay.......



Please wait while we process your payment

Sorry, you must enter a valid email address
By entering an email, you agree to our privacy policy.
Please wait while we process your payment

Sorry, you must enter a valid email address
By entering an email, you agree to our privacy policy.
Please wait while we process your payment

Your PLUS subscription has expired
Please wait while we process your payment
Please wait while we process your payment

Volumes of Solids
The application of integrals to the computation of areas in the plane can be extended to the computation of certain volumes in space, namely those of solids of revolution. A solid of revolution arises from revolving the region below the graph of a function f (x) about the x- or y-axis of the plane. A cone arises in this way from a triangular region, a sphere from a semicircular region, and a cylinder from a rectangular region. These are just a few of the possibilities for solids of revolution.
There are two primary methods for finding the volume of a solid of revolution. The shell method is applied to a solid obtained by revolving the region below the graph of a function f (x) from a to b about the y-axis. It approximates the solid with a number of thin cylindrical shells, obtained by revolving about the y-axis the thin rectangular regions used to approximate the corresponding region in the plane. This is illustrated in the figure below.
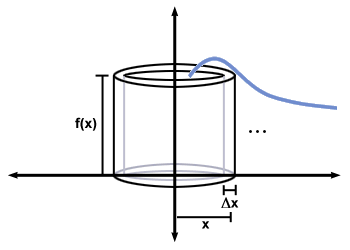
The volume of a thin cylindrical shell of radius x, thickness Δx, and height f (x) is equal to
Π(x + 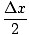 )2f (x) - Π(x - )2f (x) - Π(x - 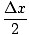 )2f (x) )2f (x) | = | Π(2xΔx)f (x) | |
| = | (2Πx)(Δxf (x)) |
Here by "cylindrical shell" we mean the region between two concentric cylinders whose radii differ only very slightly; precisely speaking, this formula is not correct for any positive thickness, but approaches the correct value as the thickness Δx shrinks to zero. Since we will ultimately consider such a limit, this formula will yield the correct volume in our application.
If we sum together the volumes of a family of such cylindrical shells, covering the entire interval from a to b, and take the limit as Δx→ 0 (and consequently as the number of cylindrical shells approaches infinity), we end up with the integral
Vol = 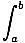 2Πxf (x)dx = 2Π 2Πxf (x)dx = 2Π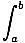 xf (x)dx xf (x)dx |
The disk method for finding volumes applies to a solid obtained by revolving the region below the graph of a function f (x) from a to b about the x-axis. Here the solid is approximated by a number of very thin disks, standing sideways with the x-axis through their centers. These disks are obtained by revolving about the x-axis the thin rectangular regions used to approximate the area of the corresponding region in the plane. This is illustrated in the figure below.
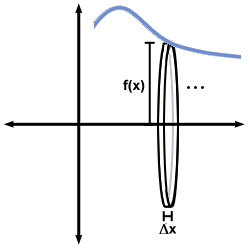
The volume of such a disk is (exactly) the area of the base times the height; hence, if the corresponding rectangle has width Δx and height f (x), the volume is equal to Πf (x)2Δx. Taking the sum of the volumes of all the disks (covering the entire interval from a to b) and taking the limit as Δx→ 0 gives the integral
Vol = 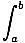 Πf (x)2dx = Π Πf (x)2dx = Π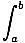 f (x)2dx f (x)2dx |
The disk method is a special case of a more general method called the cross-sectional area method. In the disc method, the quantity we end up integrating, from a to b, is Πf (x)2, the cross-sectional area of the solid when sliced by a plane through x perpendicular to the x-axis. Even when the cross-section is not a disk (as it is in the case of more general solids of revolution), there may still be a function A(x) that gives the area of the cross section obtained by slicing the solid with the plane through x and perpendicular to the x-axis. The volume of the solid is then given by
Vol = 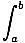 A(x)dx A(x)dx |
Please wait while we process your payment





