Angles lie in a plane. To specify the point in space where an angle lies, or where any figure exists, a plane can be assigned coordinates. Since a plane is two-dimensional, only two coordinates are required to designate a specific location for every point in the plane. One coordinate determines the length, and the other determines width. In reality, length and width are the same thing--they are used because they describe distance in two directions which are perpendicular to each other. This is all the coordinate plane is: a plane with two perpendicular axes by which distance in either of two dimensions can be measured.
The coordinate plane consists of an origin and two axes. The origin is a point. The axes are lines perpendicular to each other that intersect at the origin. Below is pictured the coordinate plane, with the origin at point O.
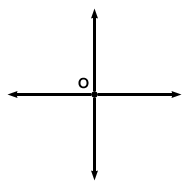
The origin is fixed, and designated as the point (0,0). Every other point is assigned an ordered pair, (x, y), according to its position relative to the origin. The two axes are named the $x$-axis and the y-axis. In most drawings, the x-axis is the horizontal axis, and the y-axis is the vertical axis, but this does not necessarily need to be the case. A point is assigned an ordered pair consisting of two real numbers: The first is the x-coordinate, which measures how far the point is from the y-axis. The second real number making up an ordered pair is the y-coordinate, which measures the distance between the point and the x-axis. Often the axes are pictured with tick marks indicating length to make it easier to measure distance. When a point is drawn into the coordinate plane and assigned an ordered pair, it is plotted. Take a gander at the plotted points below.
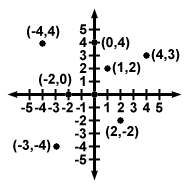
Note that some of the coordinates are negative numbers. Negative distance does not exist, but coordinates are given either positive or negative values to specify which side of the given axis they are on. In most cases, the positive direction of the x-axis points to the right, and the positive direction of the y-axis points upward. Thus, for example, points on the left of the y-axis have a negative x-coordinate. The positive directions don't always have to be these directions, though. Often, as in the diagram above, the axes will only have an arrow on the end which points in the positive direction. The other end has no arrow. This is how one can tell where the positive and negative values lie.
A plane extends in all direction without limit. So does the coordinate plane. Although there are many ways to draw the coordinate plane, it is always the same thing: a point of origin and two axes, which intersect at the origin and lie perpendicular to each other. The origin, by definition, always has the coordinates (0,0). Every other point in the plane can be measured according to the axes. Even the point (33563452143,23455434) exists and can be located in any coordinate plane; it extends without limit. Below are some other ways to draw the coordinate plane. All look different, but they are all the same coordinate plane.
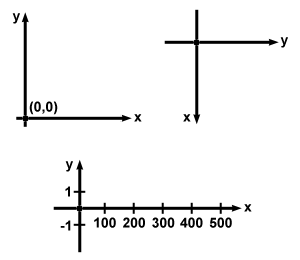
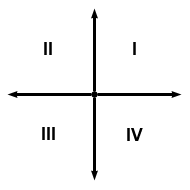
The axes of the coordinate plane divide the plane into four regions--these regions are called quadrants. The region in which the x-coordinate and the y-coordinate are both positive is called Quadrant I. Quadrant II is the region in which x < 0 and y > 0. Quadrant III is the region in which x < 0 and y < 0. Quadrant IV is the region in which x > 0 and y < 0. The quadrants are labeled in the figure below.


 payment page
payment page



