SparkNotes Plus subscription is $4.99/month or $24.99/year as selected above. The free trial period is the first 7 days of your subscription. TO CANCEL YOUR SUBSCRIPTION AND AVOID BEING CHARGED, YOU MUST CANCEL BEFORE THE END OF THE FREE TRIAL PERIOD. You may cancel your subscription on your Subscription and Billing page or contact Customer Support at custserv@bn.com. Your subscription will continue automatically once the free trial period is over. Free trial is available to new customers only.
Choose Your Plan
Payment Details
Payment Summary
Your Free Trial Starts Now!
For the next 7 days, you'll have access to awesome PLUS stuff like AP English test prep, No Fear Shakespeare translations and audio, a note-taking tool, personalized dashboard, & much more!
Thanks for creating a SparkNotes account! Continue to start your free trial.
Please wait while we process your payment
Your PLUS subscription has expired
We’d love to have you back! Renew your subscription to regain access to all of our exclusive, ad-free study tools.
One way to represent motion between points in the coordinate plane is with
vectors. A vector is essentially a line segment in a specific position,
with both length and direction, designated by an arrow on its end. The figures
below are vectors.
Figure %: Vectors
A vector can be named by a single letter, such as v. The vector v is symbolized
by a letter v with an arrow above it, like this: 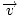. A vector
is determined by two coordinates, just like a point--one for its magnitude in
the x direction, and one for its magnitude in the y direction. The magnitude of
a vector in the x-direction is called the horizontal, or x-component of the
vector. The magnitude of a vector in the y-direction is called the vertical, or
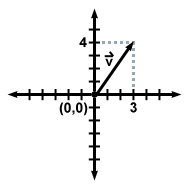
$y$-component of the vector. A vector 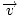with coordinates
(3,4) and origin at the origin of the coordinate plane looks like this:
Figure %:
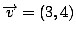
A vector has length and direction, that is all. Two vectors with the same
length and direction are the same vector. They may have origins at different
points, but they are still equal. The length of a vector is formally called its
magnitude. Given the coordinates of a vector (x, y), its magnitude is
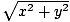. This formula is drawn from the **Pythagorean Theorem*
{math/geometry2/specialtriangles}*. The direction of a vector is only fixed
when that vector is viewed in the coordinate plane. Then, using techniques
we'll learn shortly, the direction of a vector can be calculated. Outside the
coordinate plane, directions only exist relative to one another, so a single
vector cannot have a specific direction.
Operations with Vectors
Vectors can be added and subtracted to one another, and multiplied and divided
by scalars (number with magnitude but no direction). When two vectors are added
or subtracted, the x-component of one vector is added or subtracted to the
x-component of the other, and the same is done with the y-components of the
vectors. For example, if 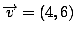and
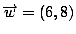, then
.
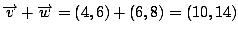When a vector is multiplied or divided by a scalar, the scalar (any
real number) is simply distributed through to both coordinates of the vector.
Hence, using the vectors defined above, 2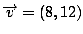 and
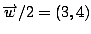. In any case, the sum, difference, product, or
quotient is still a vector.
A vector whose origin is the origin of the coordinate plane ends at the point
with the same coordinates as the vector. Because vectors have a fixed
magnitude, they always determine two points, the origin of the vector and the
endpoint. Vectors are useful mathematical tools for modeling motion and
symbolizing directed line segments.
Vectors vs. Rays
One more note is important to make in this lesson: vectors are not rays.
They are symbolized the same way--a line segment with an arrow on one
end--but they are very different things. Vectors have a specified length,
rays have infinite length. From this point on, whenever a line semgent is
drawn with an arrow on one end, assume that it is a ray. If such a figure
is a vector, it will be noted.
