payment page
Problem :
A 5kg picture frame is held up by two ropes, each inclined 45o below vertical, as shown below. What is the tension in each of the ropes?
Because the picture frame is at rest, the tension in the two ropes must
exactly counteract the gravitational force on the picture frame. Drawing
a free body diagram we can calculate the vertical components of the
tension in the ropes:
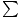F = 0, then the vertical components of the tension in the two
ropes must cancel exactly with the gravitational force:
2Ty = mgâá’2T sin 45o = (5)(9.8) = 49N. Thus:
T = 
= 34.6N. The total tension on
each rope is thus 34.6N.
Problem :
Consider a 10kg block resting on a frictionless plane inclined 30o connected by a rope through a pulley to a 10kg block hanging free, as seen in the figure below. What is the direction and magnitude of the resulting acceleration of the 2-block system?
Though this problem seems quite complex, it can be solved by simply
drawing a free body diagram for each block. Since the resulting
acceleration of each block must be of the same magnitude, we will get a
set of two equations with two unknowns, T and a. First we draw the free
body diagram:
| FG | = (10kg)(9.8) | = 98N | |
| FGâä¥ | = FGcos 30o | = 84.9N | |
| FG || | = FGsin 30o | = 49N |
The normal force is simply a reaction to the perpendicular component of the gravitational force. Thus FN = FGâä¥ = 84.9N. FN and FGâä¥ thus cancel, and the block is left with a force of 49N down the ramp, and the tension, T, up the ramp.
On block 2, there only two forces, the gravitational force and the tension. We know that FG = 98N, and we denote the tension by T. Using Newton's Second Law to combine the forces on block 1 and block 2, we have 2 equations and 2 unknowns, a and T:
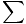 F | = ma | ||
| 10a1 | = T - 49 | ||
| 10a2 | = 98 - T |
However, we know that a1 and a2 are the same, because the two blocks are bound together by the rope. Thus we can simply equate the right side of the two equations:
Problem :
Two 10kg blocks are connected by a rope and pulley system, as in the last problem. However, there is now friction between the block and the incline, given by μs = .5 and μk = .25. Describe the resulting acceleration.
We know from the last problem that block 1 experiences a net force up the incline of 24.5 N. Since friction is present, however, there will be a static frictional force counteracting this motion. Fsmax = μsFn = (.5)(84.9) = 42.5N. Because this maximum value for the frictional force exceeds the net force of 24.5 N, the frictional force will counteract the motion of the blocks, and the 2 block system will not move. Thus a = 0 and neither block will move.
