Uniform Circular Motion: Uniform Circular Motion

Centripetal Acceleration

Before discussing the dynamics of uniform circular motion, we must explore its kinematics. Because the direction of a particle moving in a circle changes at a constant rate, it must experience uniform acceleration. But in what direction is the particle accelerated? To find this direction, we need only look at the change in velocity over a short period of time:

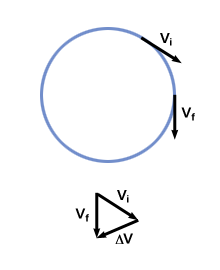
Figure %: A particle in Uniform Circular Motion

The diagram above shows the velocity vector of a particle in uniform circular motion at two instants of time. By vector addition we can see that the change in velocity, Δv, points toward the center of the circle. Since acceleration is the change in velocity over a given period of time, the consequent acceleration points in the same direction. Thus we define centripetal acceleration as an acceleration towards the center of a circular path. All objects in uniform circular motion must experience some form of uniform centripetal acceleration.

We find the magnitude of this acceleration by comparing ratios of velocity and position around the circle. Since the particle is traveling in a circular path, the ratio of the change in velocity to velocity will be the same as the ratio of the change in position to position. Thus:

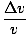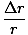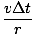Rearranging the equation,

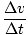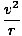Thus

a =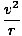

We now have a definition for both the magnitude and direction of centripetal acceleration: it always points towards the center of the circle, and has a magnitude of v²/r.

Let us examine the equation for the magnitude of centripetal acceleration more practically. Consider a ball on the end of a string, being rotated about an axis. The ball experiences uniform circular motion, and is accelerated by the tension in the string, which always points toward the axis of rotation. The magnitude of the tension of the string (and therefore the acceleration of the ball) varies according to velocity and radius. If the ball is moving at a high velocity, the equation implies, a large amount of tension is required and the ball will experience a large acceleration. If the radius is very small, the equation shows, the ball will also be accelerated more rapidly.

Centripetal Force

Centripetal force is the force that causes centripetal acceleration. By using Newton's Second Law in conjunction with the equation for centripetal acceleration, we can easily generate an expression for centripetal force.

F_c = ma =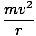

Remember also that force and acceleration will always point in the same direction. Centripetal force therefore points toward the center of the circle.

There are many physical examples of centripetal force, and we cannot completely explore each one. In the case of a car moving around a curve, the centripetal force is provided by the static frictional force of the tires of the car on the road. Even though the car is moving, the force is actually perpendicular to its motion, and is a static frictional force. In the case of an airplane turning in the air, the centripetal force is given by the lift provided by its banked wings. Finally, in the case of a planet rotating around the sun, the centripetal force is given by the gravitational attraction between the two bodies.

With a knowledge of physical forces such as tension, gravity and friction, centripetal force becomes merely an extension of Newton's Laws. It is special, however, because it is uniquely defined by the velocity and radius of the uniform circular motion. All of Newton's Laws still apply, free body diagrams are still a valid method for solving problems, and forces can still be resolved into components. Thus the most important thing to remember regarding uniform circular motion is that it is merely a subset of the larger topic of dynamics.

Previous section Next section