Gravity between planets
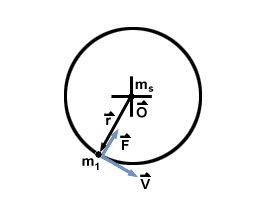
We can now use Newton's Law to derive some results concerning planets in circular orbits. Although we know from Kepler's Laws that the orbits are not circular, in most cases approximating the orbit by a circle gives satisfactory results. When two massive bodies exert a gravitational force on one another, we shall see (in the SparkNote on Orbits) that planets describe circular or elliptical paths around their common center of mass. In the case of a planet orbiting the sun, however, the sun's mass is so much greater than the planets, that the center of mass lies well within the sun, and in fact very close to its center. For this reason it is a good approximation to assume that the sun stays fixed (say at the origin) and the planets move around it. The force is then given by:
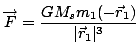 |
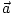 =
= 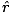
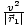 and thus
and thus  =
= 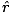
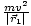 .
We can therefore write (note that in
what follows r, without the vector arrow denote the magnitude of r--that is
r = |
.
We can therefore write (note that in
what follows r, without the vector arrow denote the magnitude of r--that is
r = |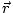 |):
|):
 = = 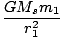 |
Rearranging we have that:
v2 = 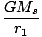 |
Thus we have derived an expression for the speed of the planet orbiting the sun. However, we can also express the speed as the distance around the orbit divided by the time taken T (the period):
v = 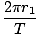 |
Squaring this and equating this with the result from above:
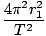 = = 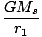 âá’T2 = âá’T2 = 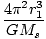 |
Thus we have derived Kepler's Third Law for circular orbits from the Universal Law of Gravitation.
Gravity near the earth
We can apply the Universal Law of Gravitation to objects near the earth also. For an object at or near the surface of the earth, the force due to gravity acts (for reasons that will become clearer in the section on Newton's Shell Theory) toward the center of the earth. That is, it acts downwards because every particle in the earth is attracting the object. The magnitude of the force on an object of mass m is given by:
F = 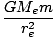 |
where re2 is the radius of the earth. Let us calculate the constant
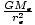 :
:
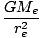 = = 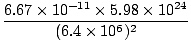 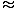 9.74 9.74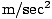 |
This is the acceleration due to gravity on the earth (the figure is usually given as
9.8 m/sec2
, but the value varies considerably at different places on the earth's surface). Thus if we rename the constants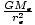 = g, then we have the familiar equation
F = mg which determines all free-fall
motion near the earth.
= g, then we have the familiar equation
F = mg which determines all free-fall
motion near the earth.
We can also calculate the value of g that an astronaut in a space shuttle would feel orbiting at a height of 200 kilometers above the earth:
| g1 | = | 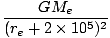 | |
| = | (6.67×10-11)(5.98×1024)(6.4×106 +2×105)-2 | ||
| = | 9.16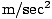 |
This small reduction in g is not sufficient to explain why the astronauts feel "weightless." In fact, this is caused by the fact that the shuttle's orbit is in fact a constant free-fall around the earth. An orbit is essentially a perpetual "falling" around a planet--since an orbiting shuttle and its occupant astronauts are falling with the same acceleration as the gravitational field, they feel no gravitational force.
Determining G
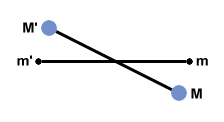
Because the gravitational force between everyday-sized objects is very small, the gravitational constant, G, is extremely difficult to measure accurately. Henry Cavendish (1731-1810) devised a clever apparatus for measuring the gravitational constant. A fiber is attached to the center of the beam to which m and m' are attached, as shown in . This is allowed to reach an equilibrium, untwisted state before, the two larger masses M and M' are lowered next to them. The gravitational force between the two pairs of masses causes the string to twist such that the amount of twisting is just balanced by the gravitational force. By appropriate calibration (knowing how much force causes how much twisting), the gravitational force may be measured. Since the masses and the distances between them may also be measured, only G remains unknown in the Universal Law of Gravitation. Thus G can be calculated from the measured quantities. Accurate measurements of G now place the value at 6.673×10-11 N.m2/kg2.


 payment page
payment page



