Problem :
Two balls of equal masses move toward each other on the x-axis. When they collide, each ball ricochets 90 degrees, such that both balls are moving away from each other on the y-axis. What can be said about the final velocity of each ball?
Initially, since both balls are moving on the x-axis, the y component of the momentum is zero. Since momentum is conserved, we can state that the momentum of each ball must be equal and opposite after the collision, as they move along the y-axis. Since both masses are equal, the velocity of each ball must be equal and opposite.
Problem :
Two pool balls traveling in opposite directions collide. One ball travels off at
an angle θ to its original velocity, as shown below. Is there any
possible way for the second ball to be completely stopped by this collision? If
so state the conditions under which this could occur.
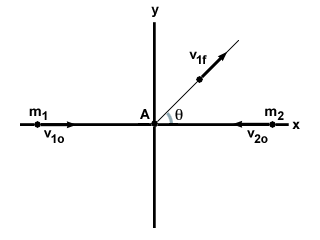
No, the second ball must also leave the collision at an angle. The first ball has a component of linear momentum in the y direction after the collision, given by v1fsinθ. Since both balls were traveling in the x direction before the collision, there was no initial momentum in the y direction. Thus, for momentum to be conserved, the second ball must travel in the negative y direction, to counteract the momentum of the first ball. If the second ball remained stationary, momentum would not be conserved.
Problem :
Two objects are traveling perpendicular to each other, one moving at 2 m/s with
a mass of 5 kg, and one moving at 3 m/s with a mass of 10 kg, as shown below.
They collide and stick together. What is the magnitude and direction of the
velocity of both objects?
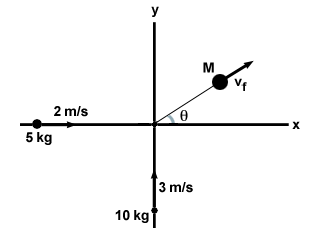
The collision is completely inelastic, and we have two variables, vf and θ, and the two equations of conservation of linear momentum. We start by relating momentum before and after the collision in the x direction:
implying that
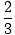
Now equating the y components,
Implying that
 =
= 
Thus
 =
= 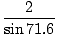 = 2.11
= 2.11
Problem :
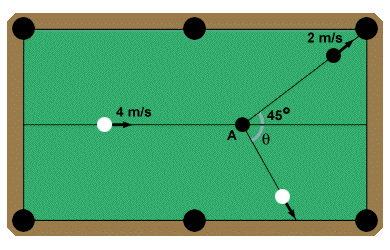
A common pool shot involves hitting a ball into a pocket from an angle. Shown
below, the cue ball hits a stationary ball at an angle of 45o, such
that it goes into the corner pocket with a speed of 2 m/s. Both balls have a
mass of .5 kg, and the cue ball is traveling at 4 m/s before the collision.
Recalling that this collision is elastic, calculate the angle with which the cue
is deflected by the collision.
To solve this problem we begin with our familiar momentum equations for both x and y components. Since we only have two variables (v1 and θ) we need not generate a third equation from conservation of kinetic energy. Thus we equate the x and y components of linear momentum before and after the collision:
| pxo | = | pxf | |
| .5(4) | = | .5v1cosθ + .5(2)cos 45 | |
| 4 | = | v1cosθ + 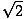 | |
| pyo | = | pyf | |
| 0 | = | 2 sin 45 - v1sinθ | |
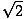 | = | v1sinθ | |
| v1 | = | 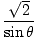 |
Here we have two equations relating θ and v1. To solve we can simply substitute our expression for v1 in terms of θ into our first equation:
| 4 | = | (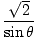 )cosθ + )cosθ + 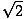 | |
4 - 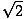 | = | 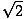 (cotθ) (cotθ) | |
| cotθ | = | 1.83 | |
| θ | = | 28.7o |
Thus the pool cue will be deflected about 30 degrees from horizontal.


 payment page
payment page



