Last section we studied head on collisions, in which both objects move on a line. Most natural collisions, however, are not head on, instead causing objects to move at an angle to their original trajectory. Consider a game of pool, in which balls are frequently hit at an angle to get them in the pockets. These kinds of collisions, though more complicated, can be solved using the same methods as those used in one dimension. An elastic collision still conserves kinetic energy and, of course, any collision conserves linear momentum. We shall examine the elastic and completely inelastic case, and show how each of these cases can be solved.
Elastic Collisions in Two Dimensions
Since the theory behind solving two dimensional collisions problems is the same
as the one dimensional case, we will simply take a general example of a two
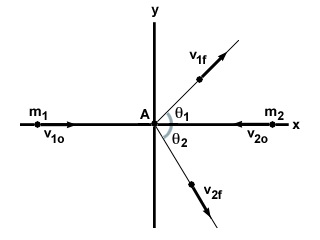
dimensional collision, and show how to solve it. Consider two particles, m1
and m2, moving toward each other with velocity v1o and v2o,
respectively. They hit in an elastic collision at an angle, and both particles
travel off at an angle to their original displacement, as shown below:
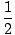 v1o2 + v1o2 + 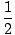 v2o2 = v2o2 = 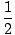 v1f2 + v1f2 + 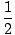 v2f2 v2f2 |
Whereas in the one dimensional problem we could only generate one equation for the conservation of linear momentum, in two dimensional problems we can generate two equations: one for the x-component and one for the y-component.
Let's start with the x-component. Our initial momentum in the x direction is given by: m1v1o - m2v2o. Note the minus sign, as the two particles are moving in opposite directions. After the collision, each particle maintains a component of their velocity in the x direction, which can be calculated using trigonometry. Thus our equation for the conservation of linear momentum in the x-direction is:
| pox | = | pfx | |
| m1v1o - m2v2o | = | m1v1fcosθ1 + m2v2fcosθ2 |
Regarding the y-component, since both particles move initially in the x direction, there is no initial linear momentum in the y direction. The final linear momentum again can be found through trigonometry, and used to form another equation:
| poy | = | pfy | |
| 0 | = | m1v1fsinθ1 + m2v2fsinθ2 |
We now have three equations: conservation of kinetic energy, and conservation of momentum in both the x and y directions. With this information, is this problem solvable? Recall that if we are given only the initial masses and velocities we are working with four unknowns: v1f, v2f, θ1 and θ2. We cannot solve for four unknowns with three equations, and must specify an additional variable. Perhaps we are trying to make a pool shot, and can tell the angle of the ball being hit by where the hole is, but would like to know where the cue ball will end up. This equation would be solvable, since with the angle the ball will take to hit the pocket we have specified another variable.
Completely Inelastic Collisions
Surprisingly enough, the completely inelastic case is easier to solve in two dimensions than the completely elastic one. To see why, we shall examine a general example of a completely inelastic collision. As we've done previously, we will count equations and variables and show that it is solvable.
The most general case of a completely inelastic collision is two particles m1
and m2 moving at an angle of θ1 to each other with velocities v1
and v2, respectively. They undergo a completely inelastic collision, and
form a single mass M with velocity vf, as shown below.
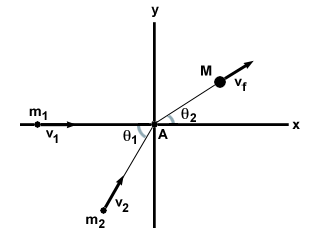
| x component: | m1v1 + m2v2cosθ1 = | Mvfcosθ2 | |
| y component: | m2v2sinθ1 = | Mvfsinθ2 |
Though we only have two equations, we also only have two unknowns, vf andθ2. Thus we can solve for any completely inelastic collision in two dimensions.
Conclusion
Our entire study of collision can be seen as simply an application of the conservation of linear momentum. So much time is spent on this topic, however, because it is such a common one, both in physics and in practical life. Collisions occur in particle physics, pool halls, car accidents, sports, and just about anything else you can think of. A thorough study of the topic will be well rewarded in practical use.


 payment page
payment page



