payment page
Problem :
What is the impulse of a force of 10 N acting on a ball for 2 seconds?
The definition of impulse is force over a time, so we have to do a simple calculation: J = FΔt = 10(2) = 20 Newton-seconds.
Problem :
Consider the last problem. The ball weighs 2 kg and is initially at rest. What is the velocity of the ball after the force has acted on it?
Recall that an impulse causes a change in linear momentum. Because the particle starts with zero velocity, it initially has a zero momentum. Thus:
| J | = | mvf - mvo | |
| 20 | = | 2vf | |
| vf | = | 10 |
Thus the ball has a final velocity of 10 m/s. This problem is the simplest form of the impulse-momentum theorem.
Problem :
A particle has linear momentum of 10 kg-m/s, and a kinetic energy of 25 J. What is the mass of the particle?
Recall that kinetic energy and momentum are related according to the following equations:
K = 
mv2 and p = mv. Since v = p/m then K = 
.
Solving for m we see that m =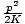 
= 
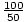= 2 kg. From
our knowledge of energy and momentum we can state the mass of the ball
from these two quantities. This method of finding the mass of a particle
is commonly used in particle physics, when particles decay too quickly to be
massed, but when their momentum and energy can be measured.
Problem :
A 2 kg bouncy ball is dropped from a height of 10 meters, hits the floor and returns to its original height. What was the change in momentum of the ball upon impact with the floor? What was the impulse provided by the floor?
To find the change in momentum of the ball we must find first the velocity
of the ball just before it hit the ground. To do so, we must rely on
the conservation of mechanical energy. The ball was dropped from a height
of 10 meters, and so had a potential energy of mgh = 10mg. This energy is
converted completely to kinetic energy by the time the ball hits the
floor. Thus:mv2 = 10mg. Solving for v, v = 
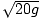= 14 m/s. Thus
the ball hits the ground with a velocity of 14 m/s.
The same argument can be made to find the speed with which the ball bounced back up. When the ball is at ground level, all of the energy of the system is kinetic energy. As the ball bounces back up, this energy gets converted to gravitational potential energy. If the ball reaches the same height it was dropped from, then, we can deduce that the ball leaves the ground with the same speed with which it hit the ground, though in a different direction. Thus the change in momentum, pf - po = 14(2) - (- 14)(2) = 56. The ball's momentum changes by 56 kg-m/s.
We are next asked to find the impulse provided by the floor. By the impulse-momentum theorem, a given impulse causes a change in momentum. Since we have already calculated our change in momentum, we already know our impulse. It is simply 56 kg-m/s.
Problem :
A ball of 2 kg is thrown straight up into the air with an initial velocity of 10 m/s. Using the impulse-momentum theorem, calculate the time of flight of the ball.
Once the ball is thrown up, it is acted on by a constant force mg. This force causes a change in momentum until the ball has reversed directions, and lands with the velocity of 10 m/s. Thus we can calculate the total change in momentum: Δp = mvf - mvo = 2(10) - 2(- 10) = 40. Now we turn to the impulse-momentum theorem to find the time of flight:
| FΔt | = | Δp | |
| mgΔt | = | 40 |
Thus:
