Problem :
Find the position of the first minimum for a single slit of width 0.04 millimeters on a screen 2 meters distant,
when light from a He-Ne laser λ = 632.8 nm is shone on the slit.
The
mth minimum is located at
sinθm = mλ/d, but in this case
m = 1 so
θ1 = sin-1(λ/d )= sin-1(632.8×10-9/4×10-5) = 0.91o.
θ is the
angle that the beams from the slit subtend at the screen, and since the distance to the screen is 2 meters, we
can write
tanθ = y/L = y/2, where
y is the displacement of the first minimum along the screen.
Thus
y = 2 tanθ = 2 tan(0.91o) = 0.032 meters, or 3.16 centimeters.
Problem :
What is the irradiance at the position of the third maximum for a single slit of width 0.02 millimeters?
The irradiance is given by
I(θ) = I0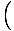
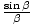
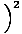, where
β = (Πd /λ)sinθ. It is given in the section lesson that the third maximum occurs when
β = ±3.4707Π. Substituting this into the above we have:
I = I0
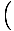
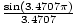
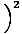= 0.082I0. Thus the third maximum is only 8% as bright as each of the
constituent waves.
Problem :
If we have a single slit 0.2 centimeters wide, a screen 1 meter distant, and the second maximum occurs at a
position 1 centimeter along the screen, what must be the wavelength of light incident on the screen?
First we must calculate
θ2, the angular position of the second maximum. We can say
tanθ = y/L = y/1 = 0.01. Thus
theta2 = 0.573o. At the position of the second maximum, the argument
of the sine in the expression for irradiance must be
β = ±2.4590Π = (Πd /lambda)sinθ2. Thus
λ = (d /2.4590)sinθ2 = (2×10-4/2.4590)sin(0.573o) = 813 nanometers.
Problem :
The Rayleigh Criterion for resolution states that two point sources are just resolved when the central
maximum from one source falls on the first minimum of the diffraction pattern from the other source. If a
car is approaching you at night with headlights 1 meter apart, how far away must you be in order to just
resolve them? (treat the headlights as single slits of width 1 millimeter, and assume the lamps are
monochromatic sodium sources of wavelength 589.29 nm).
Assume that you are standing directly in front of one of the headlights, which is a good approximation for
very long distances. The angular position of the first minimum will be where
sinθ1 = λ/d = 589.29×10-9/0.001 meters. Thus
θ1 = 0.0338o. Now, if you are a distance
L
from the car, then since you are a lateral distance of 1 meter from the other headlight,
tanθ1 = 1/L = 5.98×10-4 meters. Then,
L = 1.70×103 meters, or about 1.7 kilometers.
Problem :
A diffraction grating is a closely spaced array of apertures or obstacles forming a series of closely
spaced slits. The simplest type, in which an incoming wavefront meets alternating opaque and transparent
regions (with each opaque/transparent pair being of the same size as any other pair), is called a transmission
grating. Determine the angular position of the maxima of such a grating in terms of λ and a, the
distance between centers of adjacent slits. If light of 500 nm is incident of a slit containing 18920 slits and of
width 5 centimeters, calculate the angular position of the second maximum.
The analysis here is very much like that for
Young's Double Slit. We assume that parallel
beams of monochromatic light are incident on the slits, and that the slits are narrow enough such that
diffraction causes light to spread over a very wide angle, such that interference can occur with all
the other slits. Clearly, is the screen is very far off (compared to the width of the grating), all the beams
travel approximately the same distance to the central point, so there is a maximum there. Constructive
interference will also occur at angles
θ where light from one slit must travel a distance
mλ (
m integer) further than light from an adjacent slit. Thus if the distance between slits is
a,
this distance must be equal to
a sinθ. Thus we can write out expression for the positions of the
maxima as:
sinθ =  |
|
For the grating described,
a will be equal to
a = 0.05/18920 = 2.64×10-6. From the equation
derived:
θ2 = sin-1
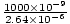
= 22.26o.
