Problem :
A mass oscillates on a spring over a rough floor. Can this motion be modeled as damped oscillation?
Though the frictional force always counteracts the motion of the mass and causes the mass to decrease its amplitude of oscillation, it cannot be considered a damping force because it is not proportional to the velocity of the mass. The kinetic friction has a constant magnitude throughout the trip, and does not change as the mass speed up or slows down. Thus this is not an example of damped oscillation.
Problem :
A mass of 2 kg oscillates on a spring with constant 50 N/m. By what factor does the frequency of oscillation decrease when a damping force with constant b = 12 is introduced?
The original angular frequency of oscillation is given by
σ =  = 5. According to our equation, the new frequency is
given
by:
= 5. According to our equation, the new frequency is
given
by:
| σâ≤ | = |  | |
| = | 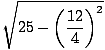 = 4 = 4 |
Thus the frequency decreases by 1 rad/s, or by 20 percent of its original value.
Problem :
In a damped oscillator the amplitude of oscillation decreases on each oscillation. How does the period of oscillation change as the amplitude decreases?
It is tempting to say that the period decreases as the amplitude decreases, since the oscillating object has less distance to travel in one cycle. The damping force, however, reduces the speed to exactly counteract this effect. Thus the period and frequency of a damped oscillator are constant throughout its motion.
Problem :
If the damping constant is large enough, an oscillating system will not go though any oscillation, but will simply slow down until it stops at the equilibrium point. In this case the angular frequency cannot be calculated, since the system does not go though any cycles. Keeping this in mind, find the maximum value of b for which oscillations do occur.
At first this problem seems quite complex. Recall, however, that we have an equation for the angular frequency of the damped oscillation. If this equation has a solution, then there must be oscillations. We must find conditions on b for which there is no solution to the equation. Recall that:

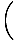 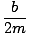  | ≤ | 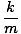 | |
| b | ≤ | 2m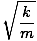 | |
| b | ≤ | 2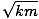 |
Thus a damped "oscillator" only really oscillates if this condition is met. Otherwise, the system goes straight to its equilibrium point.
Problem :
The gravitational attraction of the moon causes the ocean tides. This gravitational force is constant. Why, then, do some areas experience higher tides than others?
The answer lies in the study of resonance. Bays of certain shape oscillate naturally, as waves hit the shore, travel toward the center of the bay, then deflect back to the shore. The moon, then, can be seen as a driving force, which varies sinusoidally as it rotates about the earth. Thus, if the natural frequency of the bay and the frequency of the driving force are similar, the amplitude of oscillation (the size of the tide) will increase greatly. In some places the two frequencies are quite different, resulting in little change in the tide.


 payment page
payment page



