Up to this point we have only examined the special case in which the net force on an oscillating particle is always proportional to the displacement of the particle. Oftentimes, however, there are other forces in addition to this restoring force, which create more complex oscillations. Though much of the study of this motion lies in the realm of differential equations, we will give at least an introductory treatment to the topic.
Damped Harmonic Motion
In most real physical situations, an oscillation cannot go on
indefinitely.
Forces such as friction and air resistance eventually dissipate energy
and
decrease both the speed and amplitude of oscillation until the system is
at rest
at its equilibrium point. The most common dissipative force encountered
is a
damping force, which is proportional to the velocity of the object,
and
always acts in a direction opposite the velocity. In the case of the
pendulum,
air resistance always works against the motion of the pendulum,
counteracting
the gravitational force, shown below.
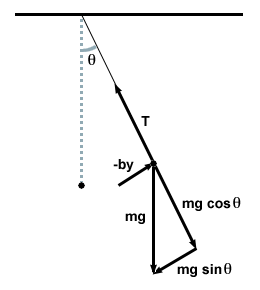
We denote the force as Fd, and relate it to the velocity of the object: Fd = - bv, where b is a positive constant of proportionality, dependent on the system. Recall that we generated the differential equation for simple harmonic motion using Newton's Second Law:
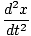
- kx - b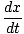 = m = m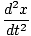 |
Unfortunately generating a solution to this equation requires more advanced mathematics than just calculus. We will simply state the final solution and discuss its implications. The position of the damped oscillating particle is given by:
| x = xme-bt/2mcos(σâ≤t) |
Where
σâ≤ =  |
Clearly this equation is a complicated one, so let's take it apart piece by piece. The most notable change from our simple harmonic equation is the presence of the exponential function, e-bt/2m. This function gradually decreases the amplitude of the oscillation until it reaches zero. We still have our cosine function, though we must calculate a new angular frequency. As we can tell by our equation for σâ≤, this frequency is smaller than with simple harmonic motion--the damping causes the particle to slow down, decreasing the frequency and increasing the period. Shown below is a graph of typical damped harmonic motion:
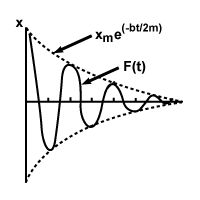
The study of damped harmonic motion could be a chapter in and of itself; we have simply given an overview of the concepts that give rise to this complex motion.
Resonance
The second example of complex harmonic motion we will examine is that of
forced
oscillations and resonance. Up to this point we have only looked at
natural
oscillations: cases in which a body is displaced and then released,
subject only
to natural restoring and frictional forces. In many cases, however, an
independent force acts on the system to drive the oscillation. Consider
a
mass
spring system in which the mass oscillates on the spring (as usual) but
the wall
to which the spring is attached oscillates at a different frequency, as
shown
below:

Usually the frequency of the external force (in this case the wall) differs from the frequency of the natural oscillation of the system. As such, the motion is quite complex, and can sometimes be chaotic. Considering the complexity, we will omit the equations governing this motion, and simply examine the special case of resonance in forced oscillations.


 payment page
payment page



