Previous Next

Period and Frequency

In simple oscillations, a particle completes a round trip in a certain period of time. This time, T, which denotes the time it takes for an oscillating particle to return to its initial position, is called the period of oscillation. We also define another concept related to time, frequency. Frequency, denoted by ν, is defined as the number of cycles per unit time and is related to period as such:

ν = 1/T    

Period, of course, is measured in seconds, while frequency is measured in Hertz (or Hz), where 1 Hz = 1 cycle/second. Angular frequency defines the number of radians per second in an oscillating system, and is denoted by σ. This may seem confusing: most oscillations don't engage in circular motion, and can't sweep out radians like in rotational motion. However, oscillating systems do complete cycles, and if we think of each cycle as containing 2Π radians, then we can define angular frequency. Again, angular frequency for oscillations may seem a bit odd for now, but it will make more sense when we compare oscillations and circular motion. For now, we can relate our three variables dealing with the cycle of oscillation:

σ = 2Πν =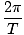    

Equipped with these variables, we can now look at the special case of the simple harmonic oscillator.

Previous page Simple Oscillating Systems page 1 Next section

Take a Study Break