As a tentative solution, we write:
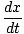 = - ab sin(bt)
= - ab sin(bt)
and
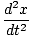 = - ab2cos(bt)
= - ab2cos(bt)
 a cos(bt) = 0
a cos(bt) = 0
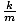 , then the equation is satisfied. Thus the
equation governing simple harmonic oscillation is:
, then the equation is satisfied. Thus the
equation governing simple harmonic oscillation is:
simple
x = a cos 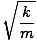 t t |
The Equation for Simple Harmonic Motion
From the equation for simple harmonic motion we can tell a lot about
the motion of a harmonic system. First of all, x is maximum when the cosine
function is equal to 1, or when x = a. Thus a in this equation is the amplitude
of oscillation, which we have already denoted by xm. Secondly, we can find
the period of oscillation of the system. At t = 0, x = xm. Also, at t = 2Π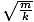 , x = xm. Since both these instances have the same
position, the time between the two gives us our period of oscillation. Thus:
, x = xm. Since both these instances have the same
position, the time between the two gives us our period of oscillation. Thus:
T = 2Π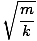 |
and
ν =  = = 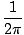 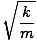 |
finally,
σ = 2Πν = 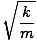 |
Note that the values of period and frequency depend only on the mass of the block and the spring constant. No matter what initial displacement is given to the block, it will oscillate at the same frequency. This concept is important. A block with a small displacement will move with slower velocity, but with the same frequency as a block with a large displacement.
Notice also that our value for σ is the same as what we called the constant b in our original equation. So now we know that a = xm and b = σ. In addition we can take the time derivative of our equation to generate a full set of equations for simple harmonic motion:
| x | = | xmcos(σt) | |
| v | = | - σxmsin(σt) | |
| a | = | - σ2xmcos(σt) |
Thus we have derived equations for the motion of a given simple harmonic system.
Energy of a Simple Harmonic Oscillator
Consider a simple harmonic oscillator completing one cycle. In the jargon of conservative vs. nonconservative forces (see Conservation of Energy the oscillator has completed a closed loop, and returns to its initial position with the same energy it began with. Thus the simple harmonic oscillator is a conservative system. Since the velocity of the oscillator does change, however, there must be an expression for the potential energy of the system, such that the total energy of the system is constant.
We already know the kinetic energy of the system at any given time:
| K | = | 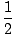 mv2 mv2 | |
| = | 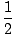 m(- σxmsin(σt))2 m(- σxmsin(σt))2 | ||
| = | 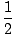 kxm2sin2(σt) kxm2sin2(σt) |
The kinetic energy has a maximum value when the potential energy is zero, and sin(σt) = 1. Thus Kmax =
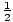 kxm. Since the potential energy
is zero at this point, this value must give the total energy of the system.
Thus, at any time, we can state that:
kxm. Since the potential energy
is zero at this point, this value must give the total energy of the system.
Thus, at any time, we can state that:
| E | = | U + K | |
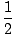 kxm2 kxm2 | = | U + 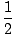 kxm2sin2(σt) kxm2sin2(σt) |
Solving for U:
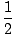 kxm2(1 - sin2(σt))
kxm2(1 - sin2(σt))
Recall that sin2a + cos2a = 1 . We can thus substitute:
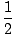 kxm2cos2(σt)
kxm2cos2(σt)
simplify
U = 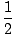 kx2 kx2 |
With this equation we have an expression for the potential energy of a simple harmonic oscillator given a displacement from equilibrium. When examined practically, this equation makes sense. Consider our example of a spring. When the spring is stretched or compressed a large amount (i.e. the block on the spring has a large magnitude for x), there is a great deal of energy stored in those springs. As the spring relaxes and accelerates the block this potential energy gets converted to kinetic energy. Shown below are three positions of the oscillating spring, and the energies associated with each position.
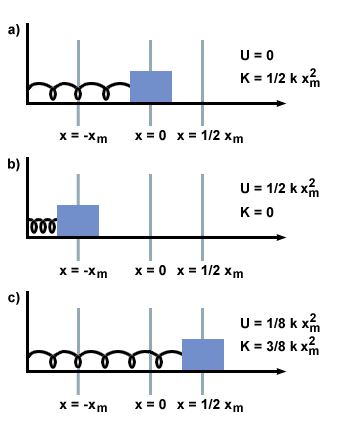
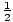 kxm2.
kxm2.
This SparkNote introducing oscillation and simple harmonic motion involved a great deal of mathematics and theoretical calculations. In the next SparkNote we explore oscillations on a more practical level, examining real physical situations and various types of oscillators.


 payment page
payment page



