Problem :
A jet engine, starting from rest, is accelerated at a rate of 5 rad/s2. After 15 seconds, what is the angular velocity of the engine? What is the total angular displacement over this period of time?
We are able to solve this problem using our basic kinematic equations. Firstly, the final angular velocity is calculated through the equation:
| μ - μo | = | σot + 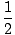 αt2 αt2 | |
| = | 0(15) + 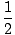 (5)(152) = 563 rad (5)(152) = 563 rad |
Problem :
Most hurricanes in the northern hemisphere rotate counterclockwise, as seen from a satellite view. In what direction does the angular velocity vector of a hurricane point?
Using the right hand rule, we curl our fingers to follow the counterclockwise path of the hurricane and, if we are viewing from above, we find that our thumb points towards us. Thus the angular velocity vector points out into space, perpendicular to the earth's surface.
Problem :
A merry-go-round is traveling initially with an angular velocity of 5 rad/s. A child pushes the merry-go-round over 10 revolutions, causing the merry-go-round to accelerate at a constant rate of 1 rad/s2. What is the final angular velocity of the merry-go-round?
Again, we use our kinematic equations. In this case, we are given σo, α and Δμ and are asked to find σf. Thus we use the following equation:
| σf2 | = | σo2 +2αΔμ | |
| = | (5)2 +2(1)(10 revolutions)(2Π rad/revolution ) | ||
| σf | = | 12.3 rad/s |
Problem :
An object moves in a circle of radius 2 m with instantaneous angular velocity of 5 rad/s and angular acceleration of 4 rad/s2. What is the magnitude of the linear acceleration felt by the object?
Because the object is moving in a circle, it experiences a radial acceleration: aRσ2r = 25(2) = 50 m/s2. In addition, the object experiences angular acceleration, resulting in an acceleration in a tangential direction: aT = αr = 8 m/s2. We know that these two values will always be perpendicular. Thus to find the magnitude of the total acceleration on the object we treat aT and aR as perpendicular components of a, just like x and y components:
 a a | = | 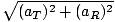 | |
| = | 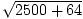 = 50.6 m/s2 = 50.6 m/s2 |
As is clear from the magnitude of the acceleration, almost all of the acceleration is in the radial direction, as the tangential acceleration is insignificant compared to the rate at which the direction of the object is changing as it moves in a circle.
Problem :
In lacrosse, a typical throw is made by rotating the stick through an angle of
approximately 90o, then releasing the ball when the stick is vertical,
as shown below. If the stick is at rest when horizontal, the length of the
stick is 1 meter, and the ball leaves the stick with a velocity of 10 m/s, what
angular acceleration must the stick experience?

To solve this equation we must use both kinematic equations and relations between angular and linear variables. We know that the ball leaves the stick with a velocity of 10 m/s, in a direction tangential to the rotation of the stick. Thus we can infer that an instant before it was released, the ball was accelerated to this speed. We can then use the relation v = σr To calculate our final angular velocity:
 = 10 rad/s
= 10 rad/s
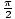 rad.
Thus we can manipulate a kinematic equation to solve for our angular
acceleration:
rad.
Thus we can manipulate a kinematic equation to solve for our angular
acceleration:
| σf2 | = | σo2 +2αμ | |
| α | = | 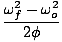 | |
| = | 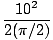 | ||
| = | 31.9 rad/s2 |
Recall that . We can assume that the angular velocity is constant, so we can use this equation to solve our problem. Each revolution corresponds to an angular displacement of radians. Thus 100 revolutions corresponds to radians. Thus:
Problem :
A car, starting from rest, accelerates for 5 seconds until its wheels are moving with an angular velocity of 1000 rad/s. What is the angular acceleration of the wheels?
Again, we can assume that the acceleration is constant, and use the following equation:
Problem :
A merry-go-round is accelerated uniformly from rest to an angular velocity of 5 rad/s in a period of 10 seconds. How many times does the merry-go-round make a complete revolution in this time?
We know that . Since we want to solve for the total angular displacement, or , we rearrange this equation: However, we are asked for the number of revolutions, not the number of radians. Since there are radians in every revolution, we divide our number by : Thus the merry-go-round revolves about 4 times in that period.


 payment page
payment page



