Problem : A train is moving directly towards you at 2×108 m/s. The (monochromatic) light on the front of the train has a wavelength of 250 nanometers in the frame of the train. What wavelength do you observe?
Using c = fλ we find the frequency of the emitted light to be 1.2×1015 Hz. The observed frequency is given by:f = 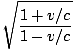 f' = f' = 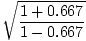 1.2×1015 = 1.2×1015 = 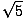 ×1.2×1015 = 2.68×1015 ×1.2×1015 = 2.68×1015 |
Thus the wavelength is λ = c/f = 3.0×108/2.68×1015 = 112 nanometers.
Problem : Light that is assumed to be from the 22.5 cm microwave Hydrogen line is measured at a frequency of 1.2×103 MHz. How fast is the galaxy from which this light was emitted receding from the earth?
This is the famous 'redshift' effect. We know that the ratio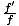 =
= 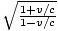 .
Because f = c/λ this must be equal to the ratio
.
Because f = c/λ this must be equal to the ratio 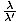 , where the unprimed
symbols denoted the frequencies and wavelengths measured on earth. Thus
, where the unprimed
symbols denoted the frequencies and wavelengths measured on earth. Thus 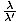 =
= 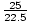 , where c/(1.2×109) = 25. Thus:
, where c/(1.2×109) = 25. Thus:
1.23 = 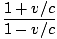 âá’1.23 - 1.23v/c = 1 + v/câá’0.23 = 2.23v/câá’v = 0.105c âá’1.23 - 1.23v/c = 1 + v/câá’0.23 = 2.23v/câá’v = 0.105c |
This is about 3.15×107 m/s.
Problem :
Consider two ultra-high-speed drag racers. One drag racer has a red stripe on the side and overtakes the
other drag racer at a relative speed of 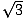 c/2. If the red stripe has wavelength 635 nanometers, what
color is the stripe as observed by the other drag racer (that is, what is the wavelength) at the exact instant
the overtaking occurs as measured in the frame of the racer-being-overtaken?
c/2. If the red stripe has wavelength 635 nanometers, what
color is the stripe as observed by the other drag racer (that is, what is the wavelength) at the exact instant
the overtaking occurs as measured in the frame of the racer-being-overtaken?
Problem : In the previous problem, what is the observed color of the stripe at the instant the overtaken drag racer observes herself being overtaken?
This corresponds to the other scenario where the faster racer has already passed but the slower one is now observing the overtaking. In this case f = f'/γ so λ = γλ' = 2×635 = 1270 nanometers (we have the same γ as calculated in the previous problem). This is in fact well out of the visible range (off the infra-red end).Problem : Explain (qualitatively if you like) why an observer moving in a circle around a stationary source observes the same Doppler effect as one of the transverse cases discussed in Section 1. Which one and what is the frequency shift? Use the fact that if an inertial observer observes the clock of an accelerating object, it is only the instantaneous speed which is important in calculating the time dilation.
This is in fact equivalent to the first transverse case described in which a stationary observer observes the light from a passing source as it is directly alongside him (that is, the case where light is coming at an angle). The instantaneous speed of the circling observer is constant at v. In the frame of the source (call it F') it emits flashes every Δt' = 1/f' seconds. But the source sees the observer's time as being dilated, thus Δt' = γΔt. The observer and source remain a constant distance from one another (because of the circular motion), so there are no longitudinal effects. The flashes are observed in F (the observer's frame) at intervals ΔT = Δt'/γ = 1/(f'γ). Thus f = f'γ which is the same result as when the moving source is just passing the observer.












