Statement
The so-called 'Twin Paradox' is one of the most famous problems in all of science. Fortunately for relativity it is not a paradox at all. As has been mentioned, Special and General Relativity are both self-consistent within themselves and within physics. We will state the twin paradox here and then describe some of the ways in which the paradox can be resolved.
The usual statement of the paradox is that one twin (call her A) remains at rest on the earth relative to another twin who flies from the earth to a distant star at a high velocity (compared to c). Call the flying twin B. B reaches the star and turns around and returns to earth. The twin on earth (A) will see B's clock running slowly due to time dilation. So if the twins compare ages back on earth, twin B should be younger. However, from B's point of view (in her reference frame) A is moving away at high speed as B moves towards the distant star and later A is moving towards B at high speed as B moves back towards the earth. According to B, then, time should run slowly for A on both legs of the trip; thus A should be younger than B! It is not possible that both twins can be right-the twins can compare clocks back on earth and either A's must show more time than B's or vice-versa (or perhaps they are the same). Who is right? Which twin is younger?
Resolution
The reasoning from A's frame is correct: twin B is younger. The simplest way to explain this is to say that in order for twin B to leave the earth and travel to a distance star she must accelerate to speed v. Then when she reaches the star she must slow down and eventually turn around and accelerate in the other direction. Finally, when B reaches the earth again she must decelerate from v to land once more on the earth. Since B's route involves acceleration, her frame cannot be considered an inertial reference frame and thus none of the reasoning applied above (such as time dilation) can be applied. To deal with the situation in B's frame we must enter into a much more complicated analysis involving accelerating frames of reference; this is the subject of General Relativity. It turns out that while the B is moving with speed v A's clock does run comparatively slow, but when B is accelerating the A's clocks run faster to such an extent that the overall elapsed time is measured as being shorter in B's frame. Thus the reasoning in A's frame is correct and B is younger.
However, we can also resolve the paradox without resorting to General Relativity. Consider B's path to the distant star lined with many lamps. The lamps flash on and off simultaneously in twin A's frame. Let the time measured between successive flashes of the lamps in A's frame be tA. What is the time between flashes in B's frame? As we learned in Heading the flashes cannot occur simultaneously in B's frame; in fact B measures the flashes ahead of him to occur earlier than the flashes behind him (B is moving towards those lamps ahead of him). Since B is always moving towards the flashes which happen earlier the time between flashes is less in B's frame. In B's frame the distance between flash-events is zero (B is at rest) so ΔxB = 0, thus ΔtA = γ(ΔtB - vΔxB/c2) gives:
ΔtB = 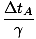 |
Thus the time between flashes is less in B's frame than in A's frame. N is the total number of flashes that B sees during her entire journey. Both twins must agree on the number of flashes seen during the journey. Thus the total time of the journey in A's frame is TA = NΔtA, and the total time in B's frame is TB = NΔtB = N(ΔtA/γ). Thus:
TB =  |
Thus the total journey time is less in B's frame and hence she is the younger twin.
All this is fine. But what about in B's frame? Why can't we employ the same analysis of A moving past
flashing lamps to show that in fact A is younger? The simple answer is that the concept of 'B's frame' is
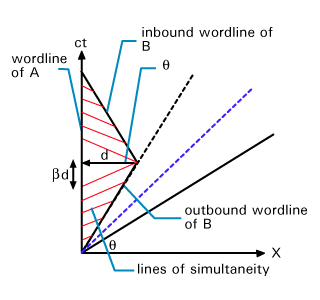
ambiguous; B in fact is in two different frame depending on her direction of travel. This can be seen on the
Minkowski diagram in :
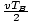 (half the total journey time times
the speed) which is also equal to d /γ due to the usual length
contraction. Thus:
(half the total journey time times
the speed) which is also equal to d /γ due to the usual length
contraction. Thus:
TB = 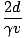 | |||
TA = 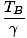 + τ = + τ = 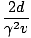 + t + t |
What is τ? We can see from that the slopes of the lines are ±v/c so the time in which A observes no flashes is ct = 2d tanθ = 2dv/c. Thus:
TA = 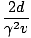 + + 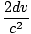 = frac2dv = frac2dv |
Comparing TA and TB we see TB = TA/γ which is the same result we arrived at above. A measures more time and B is younger.


 payment page
payment page



