Previous Next

The Entropy of an Ideal Gas

We use the relation σ = - 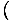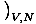to find the entropy from the free energy. Without much work, we come up with:

σ = Nlog +

The Energy of an Ideal Gas

Remember that the free energy can be defined in terms of the energy as follows: F = U - τσ. We rearrange to solve for U, and plug in our values for F and σ to find the simple result:

U = 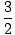Nτ

The Heat Capacity of an Ideal Gas

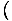
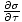
A measure of how much heat a gas can hold is the heat capacity. There are two slightly different measures of the heat capacity. One, the heat capacity at constant volume, is defined as CVâÉá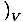. The other, the heat capacity at constant pressure, is defined as CpâÉá.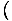

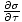
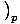The only difference between the two definitions is in what is held constant in the derivative. The results for an ideal gas can be obtained by direct substitution and differentiation for the heat capacity at constant volume, and by the thermodynamic identity for the heat capacity at constant pressure. The results are:

CV = 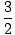N

Cp = N

Remember that these are in fundamental units, and we need to multiply by the Boltzmann constant kB to change to conventional units.

We define the ratio of the two heat capacities, Cp/CV, to be γ. For an ideal gas, γ = 5/3.

Equipartition

There is a good shortcut to find the energy of any classical system, known as equipartition. The theory states that every particle has energy equal to 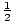τ for each degree of freedom of the particle, which can be gleaned from the number of quadratic terms in the expression for the energy.

Let us make the theory clearer by applying it to the ideal gas. Each particle in the ideal gas has classical energy equal to 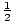mv2. Here, the velocity is a vector having 3 components. In Cartesian, there are vx, vy, and vz. Therefore each particle has energy 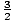τ. Summing up for all N particles in the system gives the same answer we got before, U = 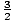Nτ.

Previous page Ideal Gas page 2 Next section

Take a Study Break