-
Bose Gas
A Bose gas is a gas consisting of bosons.
-
Boson
A boson is a particle with integer spin.
-
Classical Regime
The classical regime is that in which gases behave classically, namely without demonstrating bosonic or fermionic character. We can define the regime as f
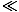 1 or n
1 or n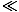 nQ.
nQ.
-
Degenerate
Term used for a gas when it is too dense to be considered as being in the classical regime, i.e. n > nQ.
-
Distribution Function
The distribution function, f, gives the average number of particles in an orbital.
-
Einstein Condensation
Also known as bose condensation, the effect of boson crowding in the ground orbital.
-
Einstein Condensation Temperature
The temperature below which Einstein Condensation significantly occurs, given by τ
 âÉá
âÉá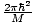
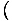
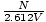
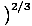 .
.
-
Equipartition
A classical shortcut that assigns to one particle energy of
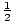 τ per degree of freedom in the classical
expression of its energy.
τ per degree of freedom in the classical
expression of its energy.
-
Fermi Energy
The Fermi energy
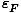 is defined as the chemical potential at
a temperature of zero: μ(τ = 0) =
is defined as the chemical potential at
a temperature of zero: μ(τ = 0) = 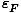 .
.
-
Fermi Gas
A Fermi gas is a gas consisting of fermions.
-
Fermion
A fermion is a particle with half-integer spin.
-
Heat Capacity
The heat capacity of a gas is a measure of how much heat the gas can hold. We define the heat capacity at constant volume to be:
CVâÉá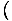
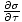
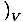 .
.
We define the heat capacity at constant pressure to be:
CpâÉá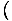
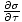
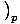 .
.
-
Ideal Gas
A gas of particles that do not interact with each other and are in the classical regime.
-
Quantum Concentration
The quantum concentration marks the concentration transition between the classical and quantum regimes, and is defined as nQ =


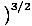 .
.
Terms
Formulas
| The classical distribution function |
f (
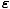 ) = e(μ- ) = e(μ- )/τ = λe- )/τ = λe- /τ /τ
|
| The chemical potential of an ideal gas |
μ = τ log
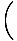 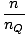  |
| The free energy of an ideal gas |
F = Nτ
 log log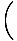 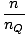  - 1 - 1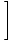 |
| The pressure of an ideal gas is given by the ideal gas law |
p =
 |
| The entropy of an ideal gas |
σ = N
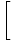 log log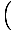 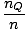 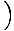 + +   |
| The energy of an ideal gas |
U =
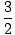 Nτ Nτ
|
| The heat capacities for an ideal gas |
CV =
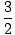 N N
Cp =
 N N
|
| The Fermi-Dirac Distribution function |
f (
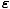 ) = ) = 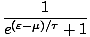 |
| The Fermi energy of a degenerate Fermi gas |
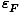 = = 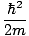 (3Π2n)2/3 (3Π2n)2/3
|
| The energy of the ground state of a Fermi gas |
Ugs =
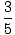 N N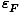 |
| The Bose-Einstein Distribution Function |
f (
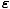 ) = ) = 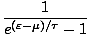 |


 payment page
payment page



