Conservation of Energy: Conservative vs. Nonconservative Forces

Gravity

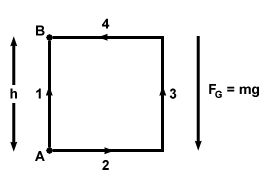
Gravity is the most common conservative force, and to demonstrate that it is conservative is relatively simple. Consider first a ball thrown up into the air. On the ball's trip upward, gravity works against the motion of the ball, producing a total work of - mgh. This negative work causes the ball to slow down until it stops, reverses direction and begins to fall. During its fall, the force of gravity is in the same direction as the motion of the ball, and the gravitational force does positive work of magnitude mgh, accelerating ball until it reaches the ground with the same speed with which it left. What is the net work done by gravity on the ball over this closed loop? Zero, as we expect by our first principle of conservative forces.

What about our second principle? Let's construct two alternative paths for a ball being thrown up into the air:

Figure %: Two different paths from A to B

Here we have path 1, a straight vertical line from A to B, and the path consisting of segments 2,3 and 4, which has vertical and horizontal components. We expect that the work done over these two segments are equal. The work over the first path is simple. The gravitational force always opposes the motion, and exerts a net work on the ball of - mgh. The work over the second path requires three calculations, one for each line segment. On segment 2, the horizontal one, the force on the ball is always perpendicular to the motion of the ball, implying that the work done on the ball over this segment is zero. The same is true for segment 4. Segment 3 is identical to segment 1, experiencing a net work of - mgh. Since the work over segment 2 and 4 is zero, the total work over the second path is - mgh, the same as the first one. We have demonstrated path independence, and thus the conservative nature of gravity.

Friction

Friction is the most common nonconservative force, and we will demonstrate why it is not conservative. Consider a crate on a rough floor, of weight W. The crate is pushed from one end of the floor to the other, a distance of h meters, and then back to its original spot. What is the net work done on the crate? At all times the friction opposes the motion of the crate, exerting a force of μ_kW at all times. Thus the total work done over the trip is simply (- 2)(μ_kW)(h) = - 2hwμ_k, clearly not equal to zero. The net work by friction over a closed path is not zero, and it is nonconservative.

Is friction path independent? We expect not, because we know it is nonconservative. To prove the suspicion, simply consider two possible ways to move a crate between two points on a rough floor. One is a straight line, one is a somewhat longer route. No matter the path, the force is the same at all times that the crate is moving. The difference, however, is that friction acts over a longer distance in the case of the second path, causing a greater net work to be done. Thus friction is not path independent, and we confirm that it is nonconservative.

The distinctions between conservative and nonconservative forces may seem somewhat arbitrary at this point. However, in the next section we will see that conservative forces, because of the properties developed in this section, allow for incredible simplification of otherwise difficult mechanics problems.

Previous page Conservative vs. Nonconservative Forces page 1 Next section