payment page
Problem :
Air resistance is a force with magnitude proportional to v2, and always acts in the opposite direction of the velocity of the particle. Is air resistance a conservative force?
Yes. Consider an object thrown into the air, reaching a maximum height, then returning to the ground, thus completing a round trip. By our first principle of conservative forces, the total work done by air resistance over this closed loop must be zero. However, since air resistance always opposes the motion of objects, it acts in the opposite direction as the displacement of the object for the entire trip. Thus the net work over the closed loop must be negative, and air resistance, much like friction, is a nonconservative force.
Problem :
A small disk of mass 4 kg moves in a circle of radius 1 m on a horizontal surface, with coefficient of kinetic friction of .25. How much work is done by friction during the completion of one revolution?
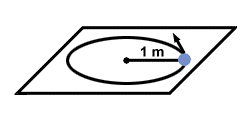
As we know with frictional force, the force exerted on the disc is constant throughout the journey, and has a value of Fk = μkFn = (.25)(4kg)(9.8m/s2) = 9.8N. At every point on the circle, this force points in the opposite direction of the velocity of the disk. Also the total distance traveled by the disc is x = 2Πr = 2Π meters. Thus the total work done is: W = Fx cosθ = (9.8N)(2Π)(cos180o) = - 61.6 Joules. Note that over this closed loop the total work done by friction is nonzero, proving again that friction is a nonconservative force.
Problem :
Consider the last problem, a small disk traveling in circle. In this case, however, there is no friction and the centripetal force is provided by a string tied to the center of the circle, and the disk. Is the force provided by the string conservative?
To decide whether or not the force is conservative, we must prove one of our two principles to be true. We know that, in the absence of other forces, the tension in the rope will remain constant, causing uniform circular motion. Thus, in one complete revolution (a closed loop) the final velocity will be the same as the initial velocity. Thus, by the Work-Energy Theorem, since there is no change in velocity, there is no net work done over the closed loop. This statement proves that the tension is, in this case, indeed a conservative force.
Problem :
Consider a ball being thrown horizontally, bouncing against a wall, then returning to its original position. Clearly gravity exerts a net downward force on the ball during the entire trip. Defend the fact that gravity is a conservative force against this fact.
It is true that there is a net downward force on the ball. However, if the ball is thrown horizontally, this force is always perpendicular to the displacement of the ball. Thus, since force and displacement are perpendicular, no net work is done on the ball, even though there is a net force. The net work over the closed loop is still zero, and gravity remains conservative.
Problem :
Calculus Based Problem Given that the force of a mass on a spring is given by Fs = - kx, calculate the net work done by the spring over one complete oscillation: from an initial displacement of d, to -d, then back to its original displacement of d. In this way confirm the fact that the spring force is conservative.
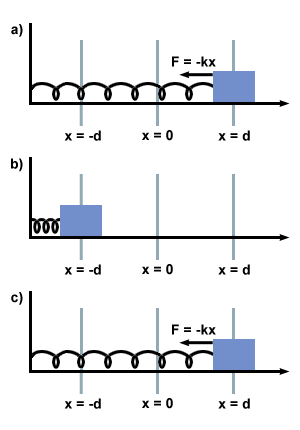
To calculate the total work done during the trip, we must evaluate the integral
W =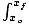 
F(x)dx. To since the mass changes directions, we must
actually evaluate two integrals: one from d to –d, and one from –d to d:
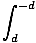-kxdx + 
-kxdx = [-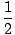 
kx2]d-d + [- 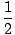kx2]-dd = 0 + 0 = 0
