-
Conservative force
Any force which conserves mechanical energy, as opposed to a nonconservative force. See statement of conservation of mechanical energy.
-
Conservative System
A system in which energy is conserved.
-
Energy
The ability to do work.
-
Kinetic Energy
The energy of motion.
-
Nonconservative Force
Any force which does not conserve mechanical energy, as opposed to a conservative force.
-
Path independence
Property of conservative forces which states that the work done on any path between two given points is the same.
-
Potential energy
The energy of configuration of a conservative system. For formulae, see Definition of potential energy, gravitational potential energy, and Definition of potential energy given a position-dependent force.
-
Total mechanical energy
The sum of the kinetic and potential energy of a conservative system. See definition of total mechanical energy.
-
Work
A force applied over a distance. For formulas, see work done by a constant force parallel to displacement and work done by any constant force, and work done by a position-dependent force.
-
Joule
The units of work, equivalent to a Newton-meter. Also units of energy.
-
Power
Work done per unit time. For formulas, see Formula for average power, Definition of instantaneous power, and formula for instantaneous power.
-
Watt
Unit of power; equal to joule/second.
Terms
Formulas
| Work done by a constant force parallel to displacement | W = Fx |
| Work done by any constant force | W = Fx cosθ |
| Work-Energy Theorem | W = ΔK |
| Formula for average power | 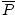 = = 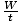 |
| Definition of instantaneous power | P = 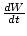 |
| Formula for instantaneous power | P = Fv cosθ |
| Work done by a position-dependent force | W = 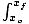 F(x)dx force. F(x)dx force.
|
| Definition of potential energy. | ΔU = - W |
| Gravitational potential energy. | UG = mgh |
| Statement of conservation of mechanical energy. | Δ(U+K) = 0 |
| Definition of total mechanical energy. | U + K = E |
| Definition of potential energy given a position-dependent force. | ΔU = - 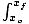 F(x)dx F(x)dx |


 payment page
payment page



