Molecular Orbitals: Molecular Orbital Theory

Homonuclear Diatomic Molecules

In atoms, as you know, electrons reside in orbitals of differing energy levels such as 1s, 2s, 3d, etc. These orbitals represent the probability distribution for finding an electron anywhere around the atom. Molecular orbital theory posits the notion that electrons in molecules likewise exist in different orbitals that give the probability of finding the electron at particular points around the molecule. To produce the set of orbitals for a molecule, we add together the valence atomic wavefunctions for the bonded atoms in the molecule. This is not as complicated as it may sound. Let's consider the bonding in homonuclear diatomic molecules--molecules of the formula A₂.

Perhaps the simplest molecule we can imagine is hydrogen, H₂. As we have discussed, to produce the molecular orbitals for hydrogen, we add together the valence atomic wavefunctions to produce the molecular orbitals for hydrogen. Each hydrogen atom in H₂ has only the 1s orbital, so we add the two 1s wavefunctions. As you have learned in your study of atomic structure, atomic wavefunctions can have either plus or minus phases--this means the value of the wavefunction y is either positive or negative. There are two ways to add the wavefunctions, either both in-phase (either both plus or both minus) or out-of-phase (one plus and the other minus). shows how atomic wavefunctions can be added together to produce molecular orbitals.

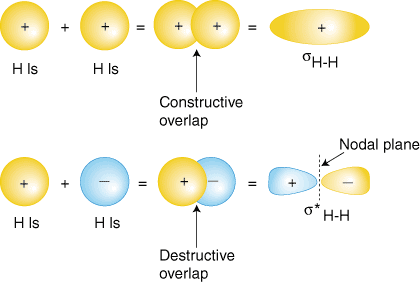
Figure %: Two 1s orbitals combine to form a bonding and an antibonding M.O.

The in-phase overlap combination (top set of orbitals in ) produces a build-up of electron density between the two nuclei which results in a lower energy for that orbital. The electrons occupying the s_H-H orbital represent the bonding pair of electrons from the Lewis structure of H₂ and is aptly named a bonding molecular orbital. The other molecular orbital produced, s^*_H-H shows a decrease in electron density between the nuclei reaching a value of zero at the midpoint between the nuclei where there is a nodal plane. Since the s^*_H-H orbital shows a decrease in bonding between the two nuclei, it is called an antibonding molecular orbital. Due to the decrease in electron density between the nuclei, the antibonding orbital is higher in energy than both the bonding orbital and the hydrogen 1s orbitals. In the molecule H₂, no electrons occupy the antibonding orbital.

To summarize these findings about the relative energies of the bonding, antibonding, and atomic orbitals, we can construct an orbital correlation diagram, shown in :

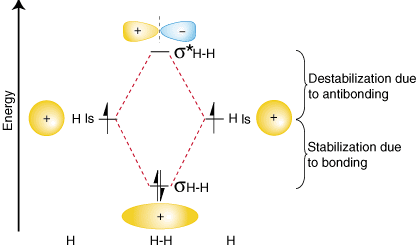
Figure %: An orbital correlation diagram for hydrogen

Notice that the orbitals of the separated atoms are written on either side of the diagram as horizontal lines at heights denoting their relative energies. The electrons in each atomic orbital are represented by arrows. In the middle of the diagram, the molecular orbitals of the molecule of interest are written. Dashed lines connect the parent atomic orbitals with the daughter molecular orbitals. In general, bonding molecular orbitals are lower in energy than either of their parent atomic orbitals. Similarly, antibonding orbitals are higher in energy than either of its parent atomic orbitals. Because we must obey the law of conservation of energy, the amount of stabilization of the bonding orbital must equal the amount of destabilization of the antibonding orbital, as shown above.

You may be wondering whether the Lewis structure and the molecular orbital treatment of the hydrogen molecule agree with one another. In fact, they do. The Lewis structure for H₂ is H-H, predicting a single bond between each hydrogen atom with two electrons in the bond. The orbital correlation diagram in predicts the same thing--two electrons fill a single bonding molecular orbital. To further demonstrate the consistency of the Lewis structures with M.O. theory, we will formalize a definition of bond order--the number of bonds between atoms in a molecule. The bond order is the difference in the number of electron pairs occupying an antibonding and a bonding molecular orbital. Because hydrogen has one electron pair in its bonding orbital and none in its antibonding orbital, molecular orbital theory predicts that H ₂ has a bond order of one--the same result that is derived from Lewis structures.