The easiest way to do stoichiometric calculations involves using conversion factors. A conversion factor is a ratio (or fraction) which represents the relationship between two different units. A conversion factor is ALWAYS equal to 1. Here are some examples of conversion factors:
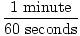 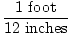 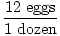 |
All these conversion factors are equal to 1. If it doesn't seem obvious at first, think about it for a second. Realize that 1 minute is equivalent to 60 seconds. Simply replace 1 minute in the fraction with its equivalent 60 seconds and it becomes clear that 60 seconds / 60 seconds = 1. Numerator and denominator are equivalent; they are just expressed differently.
As you can see it is extremely important to keep track of your units when using conversion factors. Without units, the first fraction would be 1 / 60. This is not equal to 1 and could very easily lead to wrong answers.
Furthermore, when you use units, you make it very easy to check your work. For example, perhaps you are trying to find out how many dozen eggs you have to buy to make three cakes. If you're getting an answer of 12 dozen eggs you might want to check your work. Could you even fit 12 of those cartons in your refrigerator? If you look back on your calculations you may immediately see the incorrect conversion factor: 1 egg / 12 dozen. It is easy to see that this is where the error occurred since this does NOT equal 1.
How do you use Conversion Factors?
We all know from elementary school math that if you multiply any quantity by 1 you get the same quantity back. You can do this as many times as you want. For example, 2×1 = 2, and 18×1×1×1 = 18.
Multiplication by 1 is what you do whenever you do a problem involving
conversion factors. The best way to explain how to solve using
conversion factors is to work through some simple examples.
Problem: How many days are there in 3 years? (Assume none of these
years are leap years)
Solution: Here we basically want to convert years to days. Our
conversion factor is:
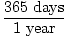 |
Since this is equivalent to 1, multiplication of this ratio with our original value will only change its units and not its magnitude. Therefore:
3 years×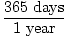 = 1, 095 days = 1, 095 days |
Notice that years is on the bottom of the conversion factor. This is VERY important. You always want to have the units of what you currently have on the bottom of the conversion factor and the units you want on the top.
Conversion Factor =  |
In this case we are multiplying our conversion factor by years. We therefore put years on the bottom of the conversion factor. When multiplied together, the resulting fraction has years in both numerator AND denominator. These units can now "cancel each other out". How? You might want to think about it like this. When you see the fraction 2 / 2, you cancel the 2s in both numerator and denominator. You can do the same thing with units.
When doing any type of problem involving conversion factors, feel free to draw a line through any unit you see on the top and bottom of the fraction to make it visually obvious that the units cancel.
3 years×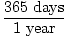 = 1, 095 days = 1, 095 days |
Canceling units in this way makes it much easier to check your work. The units you want in your answer should be the only unit not to cancel. If your calculations yield other units, which cannot be cancelled, you have made a mistake likely resulting from a missing conversion factor or an upside down conversion factor that needs to be flipped.
Here's another, slightly harder problem: How many seconds are there in
3 years?
Solution: It is easiest to use multiple conversion factors for
this problem. Starting with the units you are given, find the
conversion factor needed to express to current unit in terms of the
next smaller unit.
3 years×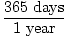 × ×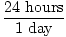 × ×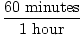 × ×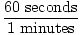 = 94, 608, 000 seconds = 94, 608, 000 seconds |


 payment page
payment page



