Let's try writing our factorial function int factorial(int n). We want to code in the n! = n*(n - 1)! functionality. Easy enough:

int factorial(int n) { return n * factorial(n-1); }

Wasn't that easy? Lets test it to make sure it works. We call factorial on a value of 3, factorial(3):

Figure %: 3! = 3 * 2!

factorial(3) returns 3 * factorial(2). But what is factorial(2)?

Figure %: 2! = 2 * 1!

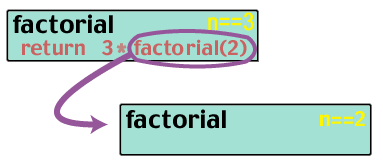
factorial(2) returns 2 * factorial(1). And what is factorial(1)?

Figure %: 1! = 1 * 0!

factorial(1) returns 1 * factorial(0). But what is factorial(0)?

Figure %: 0! = ... uh oh!

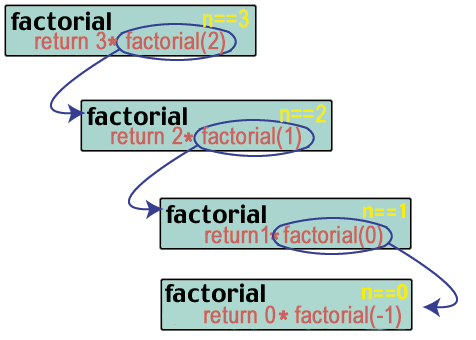
Uh oh! We messed up. Thus far

factorial(3) = 3 * factorial(2) = 3 * 2 * factorial(1) = 3 * 2 * 1 * factorial(0)
By our function definition, the factorial(0) should be 0! = 0 * factorial(-1). Wrong. This is a good time to talk about how one should write a recursive function, and what two cases must be considered when using recursive techniques.

There are four important criteria to think about when writing a recursive function.

  1. What is the base case, and can it be solved?
  2. What is the general case?
  3. Does the recursive call make the problem smaller and approach the base case?

Base Case

The base case, or halting case, of a function is the problem that we know the answer to, that can be solved without any more recursive calls. The base case is what stops the recursion from continuing on forever. Every recursive function must have at least one base case (many functions have more than one). If it doesn't, your function will not work correctly most of the time, and will most likely cause your program to crash in many situations, definitely not a desired effect.

Let's return to our factorial example from above. Remember the problem was that we never stopped the recursion process; we didn't have a base case. Luckily, the factorial function in math defines a base case for us. n! = n*(n - 1)! as long as n > 1. If n = = 1 or n = = 0, then n! = 1. The factorial function is undefined for values less than 0, so in our implementation, we'll return some error value. Using this updated definition, let's rewrite our factorial function.

int factorial(int n) { if (n<0) return 0; /* error value for inappropriate input */ else if (n<=1) return 1; /* if n==1 or n==0, n! = 1 */ else return n * factorial(n-1); /* n! = n * (n-1)! */ }

That's it! See how simple that was? Lets visualize what would happen if we were to invoke this function, for example factorial(3):

Figure %: 3! = 3*2! = 3*2*1

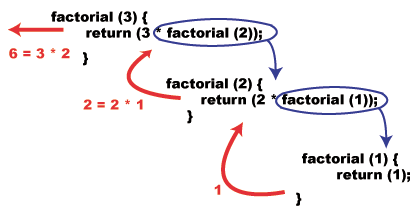
The General Case

The general case is what happens most of the time, and is where the recursive call takes place. In the case of factorial, the general case occurs when n > 1, meaning we use the equation and recursive definition n! = n*(n - 1)!.

Diminishing Size of Problem

Our third requirement for a recursive function is that the on each recursive call the problem must be approaching the base case. If the problem isn't approaching the base case, we'll never reach it and the recursion will never end. Imagine the following incorrect implementation of factorial:

/* this is incorrect */ int factorial(int n) { if (n<0) return 0; else if (n<=1) return 1; else return n * factorial(n+1); }

Note that on each recursive call, the size of n gets bigger, not smaller. Since we initially start out larger than our base cases (n==1 & n==0), we will be going away from the base cases, not towards them. Thus we will never reach them. Besides being an incorrect implementation of the factorial algorithm, this is bad recursive design. The recursively called problems should always be heading towards the base case.

Avoiding Circularity

Another problem to avoid when writing recursive functions is circularity. Circularity occurs when you reach a point in your recursion where the arguments to the function are the same as with a previous function call in the stack. If this happens you will never reach your base case, and the recursion will continue forever, or until your computer crashes, whichever comes first.

For example, let's say we had the function:

void not_smart(int value) { if (value == 1) return not_smart(2); else if (value == 2) return not_smart(1); else return 0; }

If this function is called with the value 1, then it calls itself with the value 2, which in turn calls itself with the value 1. See the circularity?

Sometimes it is hard to determine if a function is circular. Take the Syracuse problem for example, which dates back to the 1930s.

int syracuse(int n) { if (n==1) return 0; else if (n % 2 != 0) return syracuse(n/2); else return 1 + syracuse(3*n + 1); }

For small values of n, we know that this function is not circular, but we don't know if there is some special value of n out there that causes this function to become circular.

Recursion might not be the most efficient way to implement an algorithm. Each time a function is called, there is a certain amount of "overhead" that takes up memory and system resources. When a function is called from another function, all the information about the first function must be stored so that the computer can return to it after executing the new function.

The Call Stack

When a function is called, a certain amount of memory is set aside for that function to use for purposes such as storing local variables. This memory, called a frame, is also used by the computer to store information about the function such as the function's address in memory; this allows the program to return to the proper place after a function call (for example, if you write a function that calls printf(), you would like control to return to your function after printf() completes; this is made possible by the frame).

Every function has its own frame that is created when the function is called. Since functions can call other functions, often more than one function is in existence at any given time, and therefore there are multiple frames to keep track of. These frames are stored on the call stack, an area of memory devoted to holding information about currently running functions.

A stack is a LIFO data-type, meaning that the last item to enter the stack is the first item to leave, hence LIFO, Last In First Out. Compare this to a queue, or the line for the teller window at a bank, which is a FIFO data structure. The first people to enter the queue are the first people to leave it, hence FIFO, First In First Out. A useful example in understanding how a stack works is the pile of trays in your school's dining hall. The trays are stacked one on top of the other, and the last tray to be put on the stack is the first one to be taken off.

In the call stack, the frames are put on top of each other in the stack. Adhering to the LIFO principle, the last function to be called (the most recent one) is at the top of the stack while the first function to be called (which should be the main() function) resides at the bottom of the stack. When a new function is called (meaning that the function at the top of the stack calls another function), that new function's frame is pushed onto the stack and becomes the active frame. When a function finishes, its frame is destroyed and removed from the stack, returning control to the frame just below it on the stack (the new top frame).

Let's take an example. Suppose we have the following functions:

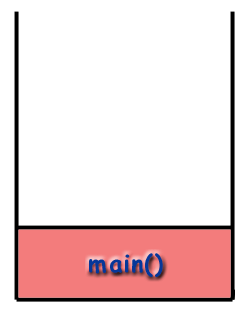
void main() { stephen(); } void stephen() { theSpark(); SparkNotes(); } void theSpark() { ... do something ... } void SparkNotes() { ... do something ... }

We can trace the flow of functions in the program by looking at the call stack. The program begins by calling main() and so the main() frame is placed on the stack.

Figure %: main() frame on the call stack
The main() function then calls the function stephen().
Figure %: main() calls stephen()
The stephen() function then calls the function theSpark().
Figure %: stephen() calls theSpark()
When the function theSpark() is finished executing, its frame is deleted from the stack and control returns to the stephen() frame.
Figure %: theSpark() finishes execution
Figure %: Control returns to stephen()
After regaining control, stephen() then calls SparkNotes().
Figure %: stephen() calls SparkNotes()
When the function SparkNotes() is finished executing, its frame is deleted from the stack and control returns to stephen().
Figure %: SparkNotes() finishes execution
Figure %: Control returns to stephen()
When stephen() is finished, its frame is deleted and control returns to main().
Figure %: stephen() is finished execution
Figure %: Control returns to main()
When the main() function is done, it is removed from the call stack. As there are no more functions on the call stack, and thus no where to return to after main() finishes, the program is finished.
Figure %: main() finishes, the call stack is empty, and the program is done

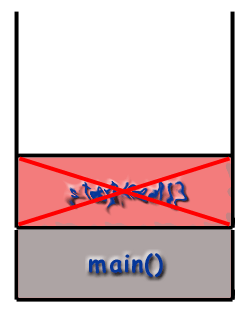
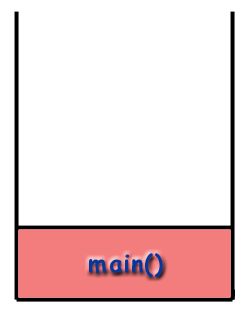
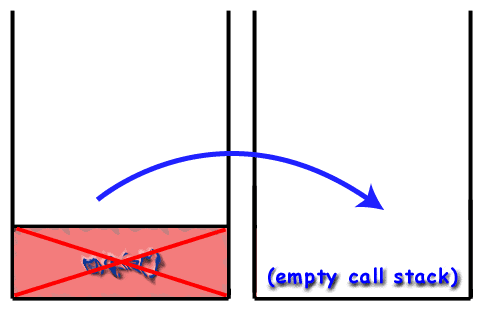
Recursion and the Call Stack

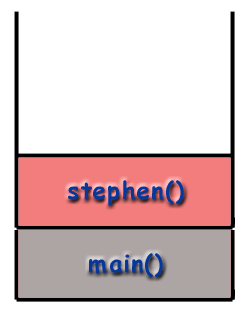
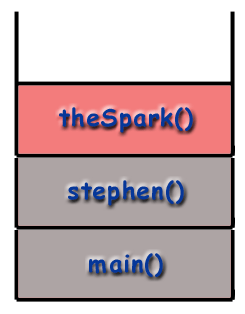
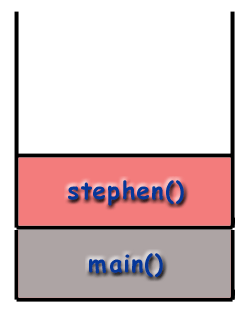
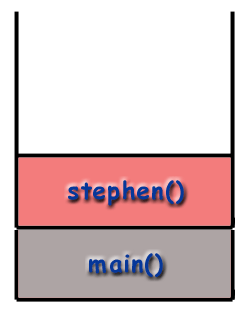
When using recursive techniques, functions "call themselves". If the function stephen() were recursive, stephen() might make a call to stephen() during the course of its execution. However, as mentioned before, it is important to realize that every function called gets its own frame, with its own local variables, its own address, etc. As far as the computer is concerned, a recursive call is just like any other call.

Changing the example from above, let's say the stephen function calls itself. When the program begins, a frame for main() is placed on the call stack. main() then calls stephen() which is placed on the stack.

Figure %: Frame for stephen() placed on the stack
stephen() then makes a recursive call to itself, creating a new frame which is placed on the stack.
Figure %: New frame for new call to stephen() placed on the stack

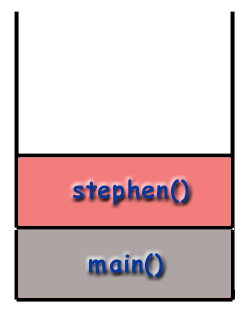
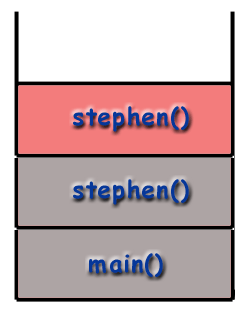
Overhead of Recursion

Imagine what happens when you call the factorial function on some large input, say 1000. The first function will be called with input 1000. It will call the factorial function on an input of 999, which will call the factorial function on an input of 998. Etc. Keeping track of the information about all active functions can use many system resources if the recursion goes many levels deep. In addition, functions take a small amount of time to be instantiated, to be set up. If you have a lot of function calls in comparison to the amount of work each one is actually doing, your program will run significantly slower.

So what can be done about this? You'll need to decide up front whether recursion is necessary. Often, you'll decide that an iterative implementation would be more efficient and almost as easy to code (sometimes they'll be easier, but rarely). It has been proven mathematically that any problem that can be solved with recursion can also be solved with iteration, and vice versa. However, there are certainly cases where recursion is a blessing, and in these instances you should not shy away from using it. As we'll see later, recursion is often a useful tool when working with data structures such as trees (if you have no experience with trees, please see the SparkNote on the subject).

As an example of how a function can be written both recursively and iteratively, let's look again to the factorial function.

We originally said that the 5! = 5*4*3*2*1 and 9! = 9*8*7*6*5*4*3*2*1. Let's use this definition instead of the recursive one to write our function iteratively. The factorial of an integer is that number multiplied by all integers smaller than it and greater than 0.

int factorial(int n) { int fact=1; /* error check */ if (n<0) return 0; /* multiply n by all numbers smaller than n and greater than 0 */ for( ; n>0; n--) fact *= n; /* return the result */ return(fact); }

This program is more efficient and should execute faster than the recursive solution above.

For mathematical problems like factorial, there is sometimes an alternative to both an iterative and a recursive implementation: a closed-form solution. A closed-form solution is a formula that involves no looping of any kind, only standard mathematical operations in a formula to compute the answer. The Fibonacci function, for example, does have a closed-form solution:

double Fib(int n){ return (5 + sqrt(5))*pow(1+sqrt(5)/2,n)/10 + (5-sqrt(5))*pow(1-sqrt(5)/2,n)/10; }

This solution and implementation uses four calls to sqrt(), two calls to pow(), two additions, two subtractions, two multiplications, and four divisions. One might argue that this is more efficient than both the recursive and iterative solutions for large values of n. Those solutions involve a lot of looping/repetition, while this solution does not. However, without the source code for pow(), it is impossible to say that this is more efficient. Most likely, the bulk of the cost of this function is in the calls to pow(). If the programmer for pow() wasn't smart about the algorithm, it could have as many as n - 1 multiplications, which would make this solution slower than the iterative, and possibly even the recursive, implementation.

Given that recursion is in general less efficient, why would we use it? There are two situations where recursion is the best solution:

  1. The problem is much more clearly solved using recursion: there are many problems where the recursive solution is clearer, cleaner, and much more understandable. As long as the efficiency is not the primary concern, or if the efficiencies of the various solutions are comparable, then you should use the recursive solution.
  2. Some problems are much easier to solve through recursion: there are some problems which do not have an easy iterative solution. Here you should use recursion. The Towers of Hanoi problem is an example of a problem where an iterative solution would be very difficult. We'll look at Towers of Hanoi in a later section of this guide.

Previous page What is Recursion? page 2 Next section

Take a Study Break