Over time the CPI changes only as the prices associated with the items in the fixed basket of goods change. In the example from Country B, the CPI increased from 100 to 141 to 182 from time period 1 to time period 2 to time period 3. The percent change in the price level from the base year to the comparison year is calculated by subtracting 100 from the CPI. In this example, the percent change in the price level from time period 1 to time period 2 is 141 - 100 = 41%. The percent change in the price level from time period 1 to time period 3 is 182 - 100 = 82%. In this way, changes in the cost of living can be calculated across time. These changes are described by the inflation rate. That is, the rate of inflation from period 1 to period 2 was 41% and the rate of inflation from period 1 to period 3 was 82%. Notice that the inflation rate can only be calculated using this method when the same base year is used for all of the CPI's involved.
While it is simple to calculate the inflation rate between the base year and a comparison year, it is a bit more difficult to calculate the rate of inflation between two comparison years. To make this calculation, first check that both comparison years use the same base year. This is necessary to ensure that the same fixed basket of goods and services is used. Next, to calculate the percentage change in the level of the CPI, subtract the CPI for the later year from the CPI for the earlier year and then divide by the CPI for the earlier year.
In the example from Country B, the CPI for period 2 was 141 and the CPI for period 3 was 182. Since the base year for these CPI calculations was period 1, we must use the method of calculating inflation that takes into account the presence of two comparison years. We need to subtract the CPI for the later year from the CPI for the earlier year and then divide by the CPI for the earlier year. That gives (182 - 141) / 141 = 0.29 or 29%. Thus, the rate of inflation from period 2 to period 3 was 29%. Notice that this method works for calculating the rate of inflation between a base year and a comparison year as well. For instance, the CPI for period 1 was 100 and the CPI for period 2 was 141. Using the formula above gives (141 - 100) / 100 = 0.41 or 41%.
Calculating Inflation Using the GDP Deflator
The other major price index used to determine the price level is the GDP deflator, a price index that shows how much of the change in the GDP from a base year is reliant on changes in the price level. As covered in the previous SparkNote, the GDP deflator is calculated by dividing the nominal GDP by the real GDP (the details for calculating the nominal GDP and the real GDP are presented in Part 1 of this SparkNote).
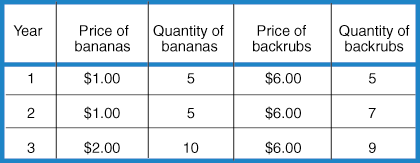
For example, let's calculate, using the table above, the GDP deflator for Country B in period 3 using period 1 as the base year. In order to find the GDP deflator, we first must determine both nominal GDP and real GDP in period 3. Nominal GDP in period 3 is (10 X $2) + (9 X $6) = $74 and real GDP in period 3 using period 1 as the base year is (10 X $1) + (9 X $6) = $64. The ratio of nominal GDP to real GDP is ($74 / $64 ) - 1 = 16%. This means that the price level rose 16% from period 1, the base year, to period 3, the comparison year. Thus, the inflation rate from period 1 to period 3 was 16%. Notice that it is important to use the earlier year that you want to compare as the base year in the calculation of real GDP.
The inflation rate calculated from the CPI and GDP deflator are usually fairly similar in value. In theory, there is a significant difference between the abilities of each index to capture consumer's consumption choices when a change in price occurs. The CPI uses a fixed basked of goods from some base year, meaning that the quantities of goods and services consumed remains the same from year to year in the eyes of the CPI, whereas the price of goods and services changes. This type of index, where the basket of goods is fixed, is called a Laspeyres index.


 payment page
payment page



