payment page
Finding the roots of higher degree polynomials is much more difficult than finding the roots of a quadratic function. A few tools do make it easier, though. 1) If r is a root of a polynomial function, then (x - r) is a factor of the polynomial. 2) Any polynomial with real coefficients can be written as the product of linear factors (of the form (x - r)) and quadratic factors which are irreducible over the real numbers. A quadratic factor that is irreducible over the reals is a quadratic function with no real solutions; that is, b2 -4ac < 0. All factors, linear and quadratic, will have real coefficients.
Two other theorems also have to do with the roots of a polynomial, Descartes' Rule of Signs, and the Rational Root Theorem.
Descartes' Rule of Signs has to do with the number of real roots possible for a given polynomial function f (x). The number of variations in a polynomial is the number of times two consecutive terms of the polynomial (a2x2 and a1x for example) have different signs. Descartes' Rule of Signs states that the number of positive real roots is less than or equal to the number of variations in the function f (x). It also states that the number of negative real roots is less than or equal to the number of variations in the function f (- x). Furthermore, in either case, the difference between the number of variations and the number of real roots will always be an even integer.
The Rational Root Theorem is another useful tool in finding the roots of a polynomial function f (x) = anxn + an-1xn-1 + ... + a2x2 + a1x + a0. If the coefficients of a polynomial are all integers, and a root of the polynomial is rational (it can be expressed as a fraction in lowest terms), the numerator of the root is a factor of a0 and the denominator of the root is a factor of an.
Using these tools, let's examine a sample polynomial function: p(x) = x4 +4x3 -8x2 - 33x - 18. There is one variation in p(x), so the number of positive roots is one. p(- x) = x4 -4x3 -7x2 + 33x - 18. p(- x) has three variations, so there are either three or one negative roots (there cannot be two because then the difference between variations and roots would not be an even integer).
Next we can use the Rational Root Theorem to look for any rational roots. The
factors of a0 = - 18 are ±1, ±2, ±3, ±6, ±9, ±18. The factors of an = 1 are ±1. Therefore the possible rational
roots are ±1, ±2, ±3, ±6, ±9, and ±18. Checking
each of these possibilities using synthetic division, we find that the only
rational roots are x = -2, 3. We can now divide the polynomial by (x + 2)(x - 3) to arrive at the quotient (x2 + 5x + 3). If this quotient were
constant, then we would have found all of the roots of the polynomial. As it
is, the quotient is a quadratic function. If it has real roots, they are
irrational. It may have no real roots, in which case we are done. Using the
quadratic formula, we find the real roots of the quadratic factor are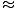 
- 0.69 and 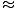- 4.30. So indeed there are three negative roots, and one
positive root, but only two rational roots. All in all there are four real
roots.
In other situations, there may be no variations in a function, in which potential roots either greater than or less than zero can be eliminated from the possibilities. In other circumstances, a quadratic factor is irreducible over the real numbers, and has only complex roots. There are also situations in which the same root factors into the polynomial twice. Although the graph of such a polynomial crosses the x-axis at that root only once, the root is counted twice. It is said to have multiplicity of two. Whenever (x - r)m is a factor of a polynomial, but (x - r)(m + 1) is not, then that root, r, is a root of multiplicity m.
Complex roots will not be discussed until after a thorough exploration of complex numbers and polar coordinates. Complex numbers are an important part of finding the roots of a polynomial, though. When a quadratic function is irreducible over the real numbers, complex roots exist. The Fundamental Theorem of Algebra states that every polynomial has at least one complex root. Furthermore, it can be proved that, including complex roots and each multiplicity counted as a different root, a polynomial with degree n always has exactly n roots. At this point, though, we'll concern ourselves exclusively with finding real roots.
