Previous Next

Periodic Functions

Calculate sin(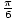) and sin() (using a calculator, for now). The answer to both is 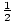. That is, the y-coordinate of a point on the terminal side of these angles is equal to one-half the distance between the point and the origin. There are many cases in which more than one angle has the same value for its sine, cosine, or some other trigonometric function. This phenomenon exists because all trigonometric functions are periodic. A periodic function is a function whose values (outputs) repeat in regular intervals. Symbolically, a periodic function looks like this: f (x + c) = f (x), for some constant c. The constant c is called the period--it is the interval at which the function has a non-repeating pattern before repeating itself again. When we graph the trigonometric functions, we'll see that the period of sine, cosine, cosecant, and secant are 2Π, and the period of tangent and cotangent is Π. For now, using reference angles, we'll learn how to calculate the value of a trigonometric function of any angle just by knowing the value of the trigonometric functions from 0 to .

Reference Angles

The use of reference angles is a way to simplify the calculation of the values of trigonometric functions at various angles. With a calculator, it is easy to calculate the value of any function at any angle. As you get more familiar with trigonometry, though, you'll memorize the values of a few simple trigonometric equations, and with reference angles, you can extend this knowledge of a few equations to many more.

A reference angle for a given angle in standard position is the positive acute angle formed by the $x$-axis and the terminal side of the given angle. Reference angles, by definition, always have a measure between 0 and . Due to the periodic nature of the trigonometric functions, the value of a trigonometric function at a given angle is always the same as its value at that angle's reference angle, except when there is a variation in sign. Because we know the signs of the functions in different quadrants, we can simplify the calculation of the value of a function at any angle to the value of the function at the reference angle for that angle.

Figure %: In each drawing, β is the reference angle for θ.

For example, sin(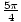) = ±sin(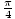). We know this because the angle 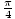is the reference angle for 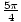. Because we know that the sine function is negative in the third quadrant, we know the whole answer: sin(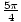) = - sin(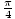). Shortly, we will become very familiar with expressions like sin(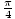), and, without much thinking, we'll know that the answer is 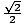. Herein lies the usefulness of reference angles: we only need to become familiar with the values of the functions from 0 to and the signs of the functions in each quadrant to be able to calculate the value of a function at any angle.

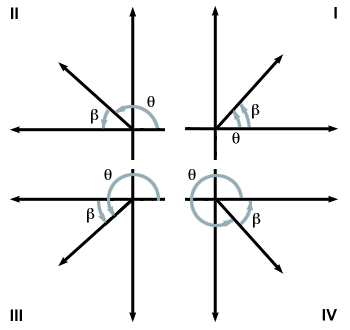
Below is a chart that will help in the easy calculation of reference angles. For angles in the first quadrant, the reference angle β is equal to the given angle θ. For angles in other quadrants, reference angles are calculated this way:

Figure %: How to calculate the reference angle β for any angle θ between 0 and 2Π radians.

For angles greater than 2Π radians, simply subtract 2Π from them, and then use the chart above to calculate the accompanying reference angle. When you become familiar with the values of certain trigonometric functions at certain common angles, like 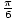and 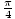, you will be capable of using reference angles to figure out the values of these functions at an infinite number of other angles.

Previous section Next section

Take a Study Break