Gravitational Potential Energy
If gravity moves an object it does work on that object. However, the amount of work done does not depend on the path over which gravity acted, but rather on the initial and final positions of the object. This means that gravity is a conservative force. We can sketch a proof of this. Imagine we have a fixed mass M and some other mass m that is moved from A to B by the gravitational force of M. It is clear that any two imaginable paths can be broken into infinitesimal steps perpendicular and parallel to the radius connecting M and m. Since gravity is a central force, the perpendicular steps make no contribution to the work, since no force is acting in this direction. Since both paths progress from A to B, the sum of their parallel-radial segments must be equal. Since the magnitude of the force is equal at equal radial distance, the work in each case must be equal.
This path independence allows us to assign a unique value to all points a distance r from a gravitating source. We call this value U(r), the gravitational potential energy. As with any potential energy, we need to define some reference point as a zero. Therefore, we define U(∞) = 0 and then:
= - 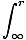 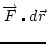 |
This makes sense as a potential energy. The integral
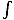 F.dr is the work
done to move a particle from infinity to a distance r away from the
gravitating object. By the work-energy
theorem the work done is the change in
kinetic energy. We have defined our gravitational potential energy as the
negative of this: as a mass moves towards the gravitating object it gains
kinetic energy (it speeds up). Since total energy is conserved, it must lose an
equivalent amount of potential energy.
F.dr is the work
done to move a particle from infinity to a distance r away from the
gravitating object. By the work-energy
theorem the work done is the change in
kinetic energy. We have defined our gravitational potential energy as the
negative of this: as a mass moves towards the gravitating object it gains
kinetic energy (it speeds up). Since total energy is conserved, it must lose an
equivalent amount of potential energy.
It remains to evaluate the integral. We can do this along any path we choose
(since they are all equivalent). We will choose the simplest path: a straight
radial path along the x-axis. In this case the force is given by 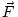 =
= 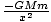
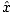 and d
and d =
= 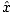 dx. Thus:
dx. Thus:
U(r) = - 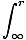 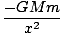 dx = dx = 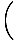  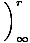 = - = - 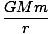 |
Where we used our definition that U(∞) = 0. The trick is that gravitational potential energy actually increases with distance. Very close to the gravitating object M, r is small and U takes on a large negative value. This value increases from a large negative value to a small negative value as the object is moved farther from M until it finally reaches zero at an infinite distance. Thus the gravitational potential energy is always negative.
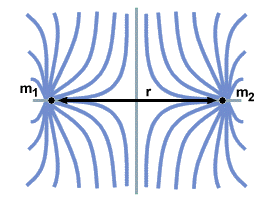
Gravitational Fields
A useful concept when dealing with forces that act at a distance is the
field. Gravitational field lines help us to
imagine what
sort of forces would act on a particle at a certain point near another
gravitating object. The direction of the field lines indicates the direction of
the force that a mass would experience if placed at a certain point, and the
density of the field lines is proportional to the strength of the force. Since
gravity is an attractive force, all field lines point towards masses.
Gravitational Potential
Occasionally, another concept is defined with respect to gravitational potential energy. We define it here primarily to avoid possible confusion with the gravitational potential energy. Gravitational potential, Φg, is defined as the potential energy that a unit mass (usually 1 kilogram) would have at any point. Mathematically:
Φg = - 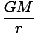 |
where M is the mass of the gravitating object. This is sometimes useful because it assigns each point in space a definite gravitational potential value, irrespective of mass.
Gravitational Potential Energy near the Earth
We can see what happens to our expression for gravitational potential energy near the earth. In this case M = Me. Consider a mass m at a distance r from the center of the earth. Its gravitational potential energy is:
U(r) = - 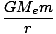 |
Similarly, the gravitational potential energy at the surface is:
U(re) = - 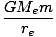 |
The difference in potential between these two points is:
ΔU = U(r)±U(re) - 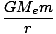 + + 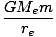 = (GMem) = (GMem)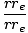 |
However, r±re is simply the height h above the earth's surface and since we are near the earth (r
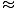 re), we can make the approximation that
rre = re2. Then we have:
re), we can make the approximation that
rre = re2. Then we have:
ΔU = 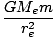 h = mgh h = mgh |
since we found in Gravity Near the Earth that g =
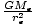 . This is the familiar result for gravitational
potential energy near the earth. Likewise gravitational potential near the
earth is Φg = gh.
. This is the familiar result for gravitational
potential energy near the earth. Likewise gravitational potential near the
earth is Φg = gh.


 payment page
payment page



