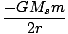payment page
-
Gravitational potential energy
Is defined by the integral:
U(r) = -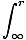 
Where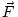
is the force due to gravity and we define U(∞) = 0. Doing the integral gives:
U(r) = -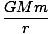 
which reduces to U = mgh near the earth. -
Gravitational potential
Is defined as the gravitational potential energy that a 1 kilogram mass would have at some point in space. It is given by:
Φg = -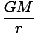 
which reduces to Φg = gh near the earth. -
Principle of Equivalence
Asserts that all types of matter fall at the same rate. That is, g for a brick is the same as g for water. This means that the inertial mass appearing in Newton's Second Law is equivalent to the gravitational mass appearing in the Universal Law of Gravitation.
-
Inertial mass
The mass mi that appears in Newton's Second LawF = mia.
-
Gravitational mass
The mass that appears in the Universal Law of Gravitation.
-
Shell Theorem
States that any spherical mass can be treated as though all its mass were concentrated at its center for the purposes of calculating gravitational force. Also, that a spherical shell of matter exerts no gravitational force on a mass inside it.
Terms
Formulae
| Energy for a circular orbit around the sun |
|
