Please wait while we process your payment
If you don't see it, please check your spam folder. Sometimes it can end up there.
If you don't see it, please check your spam folder. Sometimes it can end up there.
Please wait while we process your payment
Get instant, ad-free access to our grade-boosting study tools with a 7-day free trial!
Learn more



This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Create Account
Select Plan
Payment Info
Start 7-Day Free Trial!

Annual
2-49 accounts
$22.49/year + tax
50-99 accounts
$20.99/year + tax
Select Quantity
Price per seat
$29.99 $--.--
Subtotal
$-.--
Want 100 or more? Request a customized plan
You could save over 50%
by choosing an Annual Plan!

SAVE OVER 50%
compared to the monthly price!
| Focused-studying | ||
| PLUS Study Tools | ||
| AP® Test Prep PLUS | ||
| My PLUS Activity | ||
$22.49/month + tax
Save 25%
on 2-49 accounts
$20.99/month + tax
Save 30%
on 50-99 accounts
| Focused-studying | ||
| PLUS Study Tools | ||
| AP® Test Prep PLUS | ||
| My PLUS Activity | ||
No Fear provides access to Shakespeare for students who normally couldn’t (or wouldn’t) read his plays. It’s also a very useful tool when trying to explain Shakespeare’s wordplay!
Erika M.
I tutor high school students in a variety of subjects. Having access to the literature translations helps me to stay informed about the various assignments. Your summaries and translations are invaluable.
Kathy B.
Teaching Shakespeare to today's generation can be challenging. No Fear helps a ton with understanding the crux of the text.
Kay H.
No Fear provides access to Shakespeare for students who normally couldn’t (or wouldn’t) read his plays. It’s also a very useful tool when trying to explain Shakespeare’s wordplay!
Erika M.
I tutor high school students in a variety of subjects. Having access to the literature translations helps me to stay informed about the various assignments. Your summaries and translations are invaluable.
Kathy B.
Teaching Shakespeare to today's generation can be challenging. No Fear helps a ton with understanding the crux of the text.
Kay H.
Create Account
Select Plan
Payment Info
Start 7-Day Free Trial!
You will only be charged after the completion of the 7-day free trial.
If you cancel your account before the free trial is over, you will not be charged.
You will only be charged after the completion of the 7-day free trial. If you cancel your account before the free trial is over, you will not be charged.
Order Summary
Annual
7-day Free Trial
SparkNotes PLUS
$29.99 / year
Annual
Quantity
51
PLUS Group Discount
$29.99 $29.99 / seat
Tax
$0.00
SPARK25
-$1.25
25% Off
Total billed on Nov 7, 2024 after 7-day free trail
$29.99
Total billed
$0.00
Due Today
$0.00
Promo code
This is not a valid promo code
Card Details
By placing your order you agree to our terms of service and privacy policy.
By saving your payment information you allow SparkNotes to charge you for future payments in accordance with their terms.
Powered by stripe
Legal
Google pay.......



Please wait while we process your payment

Sorry, you must enter a valid email address
By entering an email, you agree to our privacy policy.
Please wait while we process your payment

Sorry, you must enter a valid email address
By entering an email, you agree to our privacy policy.
Please wait while we process your payment

Your PLUS subscription has expired
Please wait while we process your payment
Please wait while we process your payment

Position, Velocity, and Acceleration in One Dimension
We have already discussed examples of position functions in the previous section. We now turn our attention to velocity and acceleration functions in order to understand the role that these quantities play in describing the motion of objects. We will find that position, velocity, and acceleration are all tightly interconnected notions.
In one dimension, velocity is almost exactly the same as what we normally call speed. The speed of an object (relative to some fixed reference frame) is a measure of "how fast" the object is going--and coincides precisely with the idea of speed that we normally use in reference to a moving vehicle. Velocity in one-dimension takes into account one additional piece of information that speed, however, does not: the direction of the moving object. Once a coordinate axis has been chosen for a particular problem, the velocityv of an object moving at a speed s will either be v = s, if the object is moving in the positive direction, or v = - s, if the object is moving in the opposite (negative) direction.
More explicitly, the velocity of an object is its change in position per unit time, and is hence usually given in units such as m/s (meters per second) or km/hr (kilometers per hour). The velocity function, v(t), of an object will give the object's velocity at each instant in time--just as the speedometer of a car allows the driver to see how fast he is going. The value of the function v at a particular time t0 is also known as the instantaneous velocity of the object at time t = t0, although the word "instantaneous" here is a bit redundant and is usually used only to emphasize the distinction between the velocity of an object at a particular instant and its "average velocity" over a longer time interval. (Those familiar with elementary calculus will recognize the velocity function as the time derivative of the position function.)
Now that we have a better grasp of what velocity is, we can more precisely define its relationship to position.
We begin by writing down the formula for average velocity. The average velocity of an object with position function x(t) over the time interval (t0, t1) is given by:
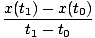
As the time intervals get smaller and smaller in the equation for average velocity, we approach the instantaneous velocity of an object. The formula we arrive at for the velocity of an object with position function x(t) at a particular instant of time t is thus:
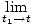
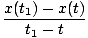
Please wait while we process your payment





