In the previous section on position, velocity, and acceleration we found that motion with constant acceleration is given by position functions of the form:
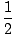 at2 + v0t + x0
at2 + v0t + x0
Free Fall
The first application we will discuss is that of objects in free fall. In general, the acceleration of an object in the earth's gravitational field is not constant. If the object is far away, it will experience a weaker gravitational force than if it is close by. Near the surface of the earth, however, the acceleration due to gravity is approximately constant--and is the same value regardless of the mass of the object (i.e., in the absence of friction from wind resistance, a feather and a grand piano fall at exactly the same rate). This is why we can use our equations for constant acceleration to describe objects in free fall near the earth's surface. The value of this acceleration is a = 9.8 m/s2. From now on, however, we will denote this value by g, where g is understood to be the constant 9.8 m/s2. (Notice that this is not valid at large distances from the surface of the earth: the moon, for instance, does not accelerate towards us at 9.8 m/s2.)
The equations describing an object moving perpendicular to the surface of the earth (i.e. up and down) are now easy to write. If we locate the origin of our coordinates right at the earth's surface, and denote the positive direction as that which points upwards, we find that:
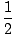 gt2 + v0t + x0
gt2 + v0t + x0
How does this relate to an object in free fall? Well, if you stand at the top of a tower with height h and let go of an object, the initial velocity of the object is v0 = 0, while the initial position is x0 = h. Plugging these values into the above equation we find that the motion of an object falling freely from a height h is given by:
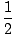 gt2 + h
gt2 + h
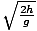 the object hits the ground (i.e. reaches the position
0).
the object hits the ground (i.e. reaches the position
0).
Firing a Bullet Directly Upwards
The equation
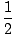 gt2 + v0t + x0
gt2 + v0t + x0
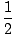 gt2 + v0t
gt2 + v0t


 payment page
payment page



